#11 sin、cosの定義が面白い！

　高校1年生で初めてsin、cosを勉強すると、難しい数式扱ってる気分になってワクワクするものですよね。まあ、もしかしたら意味不明なやつが出てきてやりたくないーって思ってしまう人もいるかもしれませんが（笑）

　ところでsin、cosの話の序盤は理解できるのに、単位円が出てきた途端「もう無理！」って言う人はいませんか？今回はそんな人に向けた記事です。

　今回の要点を先にお伝えすると、sin,cosの定義は段階的に変化するということです。単位円が登場するタイミングで定義が変化するため、そこでつまずく人が多いのです。これをふまえた上で以下の話を読んでみてください。これから順に説明する1)、2)の定義は、同じではありません。それでは、どのように変化するかをチェックしてくださいね。

1)直角三角形を用いた定義

 sin,cosとの初めての出会い…

数学1の図形と計量の単元ではまず直角三角形を用いた定義が登場します。

上の図のように直角三角形ABCがあるとします。

とすると、と定義します。

※覚え方

上の図のように筆記体のs、c、tの書き始めの方が分母になり、書き終わりの方が分子になります。

　＊sの場合は書き始めが斜辺AC、書き終わりがABですので、です。

　この定義では、θを直角三角形の一つの角度として設定していますので、の範囲での定義になります。

　しかし、欲張りな人は言いました。「これではθの範囲がせまい。  の範囲外の角度についても、sin、cosの値を考えたい」

そんな願いを叶えるために登場するのが次の、単位円による定義なのです。

2)単位円を用いた定義

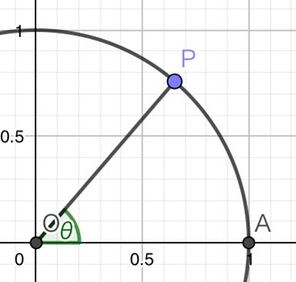
　上の図のような半径1の単位円において、点Aを座標(1,0)、点Pを単位円周上の点で、として、この時の点Pの座標を(cosθ,sinθ)と定義します。つまりこのとき、sin,cos を辺の比ではなく点Ｐの座標として定義したわけです。

※この時のθは点Pと点Aが重なる時を0として、点Ｐを反時計回りに移動するとθの値は正の数として増加し、時計回りに動かすとマイナスになります。

　この定義ならθは何度まで回すことができますか？

θを二週目、三週目…と回すことによって2πを超える角度だってsin,cosの値が得られます。つまり回し放題！の範囲に限定されず、θはどんなに大きくても、小さくても大丈夫。

定義1)では  に限られていたθが、定義2)になると角度の制限がなくなりました。角度θを制限から解放すること。これこそが定義を変える理由なのです。

さて、同じsin cos について1)と2)の異なる定義が登場しましたが、ここからはこれら２つの定義の関係性を見ていきましょう。

定義1)で求めたsin60°の値と定義2)で求めたsin60°の値が違ったりしたら困りますよね？その点をチェックしていきます。

上図のように点Pからx軸に下ろした垂線の足を点Hとします。

　単位円を用いた定義２では点Pの座標は(cosθ,sinθ)ですので、OH=cosθ、PH=sinθになりますね。

　直角三角形を用いた定義１では、 となります。

　定義１でも定義２でもcosθ=OH、sinθ=PH となっていますので、sin、cosの値は同じと言えます。つまり、 の範囲においては定義1)で考えても定義2)で考えてもsin,cosの値は同じになるのです。当たり前に思うかもしれませんが、これはかなり大事なこと。これで、安心して使えますね(^^)

＊sin,cosが一致するということはの値をとるtanも一致しています。

　定義の変化に気づかずに定義１のまま単位円に突入してしまうので、わからなくなってしまうのです。単位円が出てくるタイミングでsin,cosは再定義され、の制限から解放される。「定義１と定義２は違う」ということを理解してもらえましたか？

＊ちなみに大学レベルではθをさらに複素数の範囲まで解放するため、また別の定義が追加されます。

　三角関数マスターになるための第一歩として、sin,cosの定義をしっかりと理解してもらえると嬉しいです。