医学生Gの数学ノート

スキマ時間で読める数学の記事を数学塾講師経験のあるメンバーがお届けします！

#16 合成公式はsinだけじゃないんです！

高2

お久しぶりです。医学生Gです。

今日は多忙のためちょっとテンション高めでお送りします。簡単な内容の記事を書くつもりが、思いついたことをあれこれ書いていると意外にハイレベルな記事となってしまいました。無理だと思ったら適宜飛ばしながら読んでください。それでは本日の講義、スタートです！

 

数II 三角関数の単元では合成公式を学習すると思います。

sinとcosの和がsinのみの式に変幻するやつです。覚えていますか？

教科書ではこのsin合成がメインになっていると思いますが実はcos合成というものもあるんです。今回は普段は登場しないcos合成の話も含めて、合成公式のいろいろな魅力をご紹介します。

 

1) まずはsin合成の復習から。

a\sin{\theta}+b\cos{\theta}=\sqrt{a^2+b^2}\sin(\theta+\alpha)

というやつですね。これを導出しておきます。

ポイントは3つです。

・\sqrt{a^2+b^2}を無理やりくくり出すこと

・三角形をイメージして新たな角度を登場させること

・加法定理を逆向きに使うこと

それではいってみましょう！

 

a\sin\theta+b\cos\theta

\displaystyle=\sqrt{a^2+b^2}(\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\frac{b}{\sqrt{a^2+b^2}}\cos\theta) ←無理やりくくり出す

=\sqrt{a^2+b^2}(\cos\alpha\sin\theta+\sin\alpha\cos\theta) ←αが登場

=\sqrt{a^2+b^2}\sin(\theta+\alpha) ←加法定理

 

αが登場する部分は次のような直角三角形を考えています

f:id:sarugorirag:20190917093152j:plain



 a,bの値に合わせて適切な角度αを自分で新たに登場させたわけです。

問題の解答を書くときには、勝手に登場させた角度αについて、

“但しαは\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}を満たす鋭角”

などというように紹介をしておくことがマナーです。

                  (注)いつも鋭角になるとは限りません！

 

 

それでは前置きはこれくらいにして、cos合成の話を始めます！

cos合成の式は   \displaystyle{c\cos\theta+d\sin\theta=\sqrt{c^2+d^2}\cos(\theta-\beta)}   です。

 

 2) cos合成の導出 その1

まずは基本的な導出からやってみようと思います。

先ほどのsin合成と同様の手順で導きますので、どこが同じでどこが異なるかをチェックしながらみてくださいね。

c\cos\theta+d\sin\theta ←cos sin の順番に並べた方がわかりやすいと思います

\displaystyle=\sqrt{c^2+d^2}(\frac{c}{\sqrt{c^2+d^2}}\cos\theta+\frac{d}{\sqrt{c^2+d^2}}\sin\theta) ←無理やりくくり出す

=\sqrt{c^2+d^2}(\cos\beta\cos\theta+\sin\beta\sin\theta) ←βが登場

=\sqrt{c^2+d^2}\cos(\theta-\beta) ←加法定理

今回βを登場させるにあたって考えた直角三角形は次のようなものです。

f:id:sarugorirag:20190917093217j:plain



3) cos合成の導出 その2

先ほどとは異なるcos合成の導出の方法として、ベクトルを用いたものをご紹介します。ベクトルをまだ習っていない方には少し難しいかもしれませんが、ベクトルを習得している人にとっては美しすぎて感動するレベルですのでお付き合いください。

 

少しだけベクトルの復習をしておきましょう。

2つのベクトル\vec{a}=(x_a,y_a) と \vec{b}=(x_b,y_b) について

これらのなす角を\theta とすると

内積は\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta

と定義されますがベクトルの成分を用いて

\vec{a}\cdot\vec{b}=x_ax_b+y_ay_b とも計算できます。

つまりベクトルの内積の計算方法は２つあるということです。

 

それではこれを踏まえてcos合成の導出をしてみましょう。

おもむろに２つのベクトルを

\vec{p}=(c,d) ,  \vec{e}=(\cos\theta,\sin\theta) とおき、

それぞれがx軸となす角を \beta , \theta とします。

するとこれら２つのベクトルのなす角は(\beta-\theta)となりますね。

 

f:id:sarugorirag:20190918090905j:plain


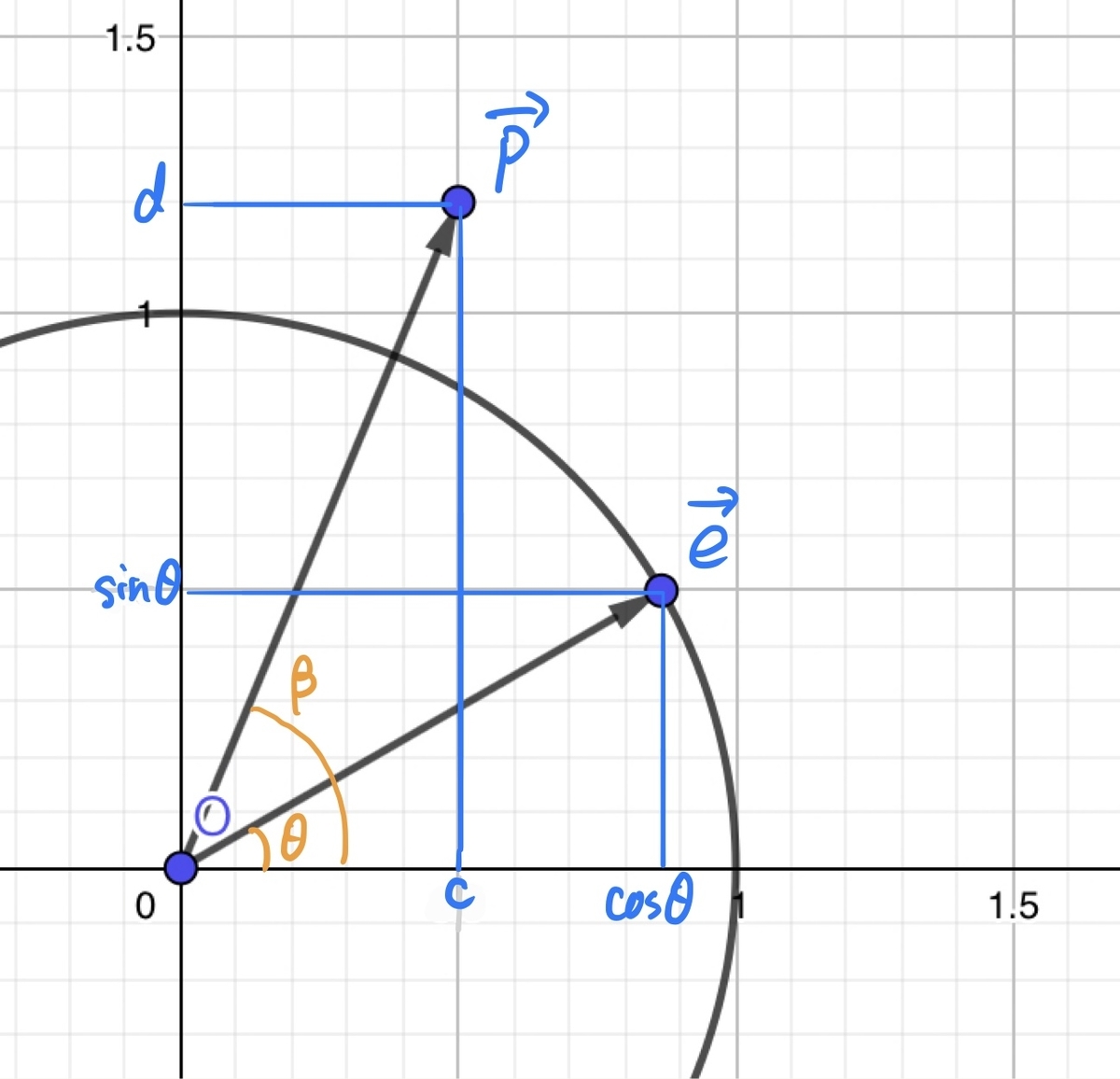
それでは内積を計算します。

定義で計算すると

\vec{p}\cdot\vec{e}=|\vec{p}||\vec{e}|\cos(\beta-\theta)

         =\sqrt{c^2+b^2}\sqrt{cos^2\theta+sin^2\theta}\cos(\beta-\theta)

         =\sqrt{c^2+b^2}\cos(\beta-\theta)

         =\sqrt{c^2+b^2}\cos(\theta-\beta)\cdots①  (∵\cos(-\theta)=\cos\theta)

成分で計算すると

\vec{p}\cdot\vec{e}=c\cos\theta+d\sin\theta\cdots②

①=②より、

c\cos\theta+d\sin\theta=\sqrt{c^2+d^2}\cos(\theta-\beta)

となります。

やってることは内積の計算だけ！ シビれますよねぇ。

美しい導出だと思いませんか？笑

 

他に幾何的な導出の方法などもありますので興味がある人は調べてみてくださいね。

 

 

4) cos合成を知っておくメリット

 cos合成を知っておくと、sinにまとめるかcosにまとめるかを自由に選択することができます。

例えば最大最小をもとめる場合を考えると、単位円においてsinの場合大小を上下(y軸)方向で考えますが、cosでは左右(x軸)方向で考えます。このようにsinとcosにはそれぞれ性格が異なる部分がありますので、状況に応じて使い分けることができると武器になりますね。

 

そして最大のメリットは数Ⅲで登場する極方程式と相性が抜群に良いことではないでしょうか。

円、放物線、楕円、双曲線など焦点を持つ曲線は通常cosを含む極方程式で表されます。(離心率eが頭に浮かんだ人はバッチリですね。)

直線の式もcosを含む極方程式で表すことができます。

よって高校範囲で登場する極方程式に三角関数が含まれているならば、十中八九それはcosなんですよね。（  ※ sinで表せないこともないですが、式が汚くなることが多いです。）

だったら、最初からcosにまとめた方が楽じゃないですか？

 

例として、x,yを用いて表されている直線の方程式をr,θを用いる極方程式に変換する場合を考えてみましょう。

x+\sqrt{3}y=2

⇨r\cos\theta+\sqrt{3}r\sin\theta=2

    r(\cos\theta+\sqrt{3}\sin\theta)=2

    r(2\cos(\theta-\frac{\pi}{3}))=2

    r\cos(\theta-\frac{\pi}{3})=1

という感じです。合成のみで式が整いましたよね。

数Ⅲを学習される方はcos合成ができると便利だと思います。

 

5) 合成の本質

合成公式を使ったsinとcosの合成は、“波の合成”に他なりません。このことを説明しておきます。

例として sin(x)+cos(x) をsin合成すると\sqrt{2}\sin(x+\frac{\pi}{4}) となるのですが、これらのグラフを見てみましょう。

f:id:sarugorirag:20190918195403j:plain

青がy=sin(x) ,緑がy=cos(x) ,オレンジがy=\sqrt{2}\sin(x+\frac{\pi}{4}) のグラフです。

縦に見てみると、オレンジが青と緑の高さの合計を表していませんか？

このように、合成公式というのは波の足し算を式で表しているだけのものなのです。

ちなみにこの“波の合成”は物理現象として海面上などで実際に起きています。自然現象の謎を解き明かす為に数学が有効となる良い例ですね。

 

あと、cos合成したらどうなるの？という疑問にお答えしておきます。

sin(x)+cos(x)をcos合成すると\sqrt{2}\cos(x-\frac{\pi}{4})となりsin合成とは一見違った式が出てきますが、\sin(\frac{\pi}{2}-\theta)=\cos\theta と \cos(-\theta)=\cos\theta を使って変形すると

\sqrt{2}\sin(x+\frac{\pi}{4})      ←sin合成

=\sqrt{2}\sin(\frac{\pi}{2}-(-x+\frac{\pi}{4}))

=\sqrt{2}\cos(-x+\frac{\pi}{4})

=\sqrt{2}\cos(x-\frac{\pi}{4})      ←cos合成

となるので、sin合成で得られた式とcos合成で得られた式は見た目は違えど同じ波を表す同一のものであることがわかります。同じ結果になるからこそ、sin合成とcos合成、好きな方を使って良いということになるのですね。

 

 

今回の内容は以上になります。cos合成は知る人ぞ知る有名な裏技ですので知っておいて損はないでしょう。実際にcos合成で瞬殺できる問題がセンター試験で過去に出題されています。

   ここまで読んでチンプンカンプンだっだ人は今はわからなくてもいいですが、要するに三角関数はいろいろな性質を併せ持ち、数学や物理などのさまざまな分野と関連している非常にExcitingなものだということです。三角関数を極めれば数式の見え方が変わってくると思いますので重点的に勉強してくださいね。それでは。おやすみなさい。