#13 (90°±θ)、(180°±θ)の問題を解く
こんにちは、医学生Gです。今回の記事はつまずく人が多いと思われる (90°±θ)、(180°±θ)みたいな角度の三角比について話をしていこうかと思います。
この (90°±θ)、(180°±θ)、知ってる人もいるかとは思いますが、暗記しなくても導くことができるのです。実際暗記の嫌いな私も導いて考えていましたので是非参考にしてみてください。
1)〜4)の例題を通してその手順を説明していきます。
*今回は0)〜4)まであります。図が手書きのため、読みにくかったらすみません。
0)単位円の定義の復習
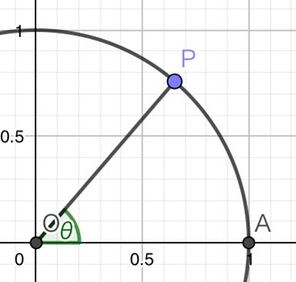
上の図のような半径1の単位円において、点Aを座標(1,0)、点Pを単位円周上の点で、として、この時の点Pの座標を(cosθ,sinθ)と定義しましたね。覚えていましたか?以下、これを使ってやりますので記憶が曖昧!って人は#11を確認してください。
1)cos(90°-θ)

上の図を参考にしながら6つのステップで解いていきましょう。
*点Aの座標を(cosθ,sinθ)としておきますね。
①90°-θの点はどこか
90°からθを引いた角度の点ですよね。単位円上の点をy軸からθだけ時計回りに動かした点、上図だと点Cのことです。
②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る
点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形CODの2つの直角三角形ができましたね。
③合同な三角形を見つけよう
先ほど作った直角三角形は実は合同な三角形であり△OAB≡△CODとなります。
どちらも内角が 90°,θ,(90°-θ) となっています。確認してみてください。
④求めたい数値と同じ値となる辺を探す
今回はcos(90°-θ)の値が知りたいですので点Cのx座標の値と同じになる辺を探してくれば良いのです。(cosはx座標として定義されるんでしたよね。) そうなると辺ODの長さが点Cのx座標の値と一致しますよね。ということは、合同な三角形である△OABにおける辺ABの値とも一致します。
⑤ ④で見つけた辺の長さを求める
辺ODの長さは辺ABの長さと一致しているというのは④でわかりました。辺ABの長さは点Aのy座標の値と一致してますので、AB=sinθ
AB=ODよりOD=sinθ と分かります。
⑥ ⑤で見つけた値と今求めようとしている値を一致させる
今求めたいのはcos(90°-θ)の値、つまり点Cのx座標の値です。④でも書いてる通り点Cのx座標の値は辺ODの長さと一致します。つまり、⑤より cos(90°-θ)=OD=sinθ となります。
長々と①〜⑥まで書きましたが慣れてくると10秒くらいでできますので是非参考にしてください。
2)sin(180°-θ)

上図を参考にして1)と同じことをしていきます。
*点Aの座標を(cosθ,sinθ)としておきますね。
①180°-θの点はどこか
180°-θはx軸からθだけ時計回りに引いた上図の点Cのところになります。
②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る
点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形OCDの2つの直角三角形ができましたね。
③合同な三角形を見つけよう
今回の合同な三角形は △OABと△OCD です。
④ 今求めたい数値と同じ値となる辺を探す
今回はsin(180°-θ)の値が知りたいですので点Cのy座標の値と同じになる辺を探してくれば良いのです。そうなると辺CDの長さが点Cのy座標の値と一致しますよね。ということは、合同な三角形である△OABにおける辺ABの値とも一致します。
⑤ ④で見つけた辺の長さを求める
辺CDの長さは辺ABの長さと一致しているというのは④でわかりました。辺ABの長さは点Aのy座標の値と一致してますので、AB=sinθ
AB=CDよりCD=sinθとなります。
⑥ ⑤で見つけた値と今求めようとしている値を一致させる
今求めたいのはsin(180°-θ)、つまり点Cのy座標の値です。④でも書いてる通り点Cのy座標の値は辺CDの長さと一致します。つまり、⑤よりsin(180°-θ)=CD=sinθになりますね。
3)cos(90°+θ)

上図を参考にしてまた同じことをいていきます。
*点Aの座標を(cosθ,sinθ)としておきますね。
①90°+θの点はどこか
90°+θは元の△OABのに90°だけ足した点です。上図の点Cがそうですね。
②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る
点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形OCDの2つの直角三角形ができましたね。
③合同な三角形を見つけよう
今回の合同な三角形は△OABと△COD です。
④今求めたい数値と同じ値となる辺を探す
今回はcos(90°+θ)の値が知りたいですので点Cのx座標の絶対値と同じになる辺を探してくれば良いのです。なぜ今回は絶対値をとるかと言いますと、点Cのx座標の値は今回はマイナスであり、辺の長さにマイナスは存在しないからです。なんとなくわかってもらえればかまいません。すると辺ODの長さが点Cのx座標の絶対値と一致しますよね。ということは、合同な三角形である△OABでいう辺ABの値とも一致します。
⑤ ④で見つけた辺の長さを求める
辺ODの長さは辺ABの長さと一致しているというのは④でわかりました。辺ABの長さは点Aのy座標の値と一致してますので、AB=sinθ、AB=ODよりOD=sinθとなります。
⑥ ⑤で見つけた値と今求めようとしている値を一致させる
今求めたいのはcos(90°+θ)、つまり点Cのx座標の絶対値です。④でも書いてる通り点Cのx座標の値は辺ODの長さと一致します。ただし、cos(90°+θ)の座標は負の値ですのでここでマイナスをつけるのを忘れないようにしましょう。今回は、⑤よりcos(90°+θ)=-OD=-sinθになりますね。
0°<θ<180°の範囲だったらsinの方は常に正の値ですので、何も考えずに辺の長さで求めることができますが、cosは90°<θ<180°の範囲は負の値を取りますので、もし最初に置いた点が負のところにあったら最後にマイナスを付け忘れないように注意しましょう。
4)tan(90°-θ)

tanはsin、cosと違って座標じゃないからできないじゃん!って思った人いますか?そんな人も心配しなくて大丈夫!ほとんど同じやり方でtanも求めることができます。
まず、tanの値は何かと言いますとtanは傾きの大きさです。上図で言いますとtanθの値はOAの傾きと一致します。今回はこれを利用していきます。やる過程はだいたい一緒ですので同じところは軽く飛ばしてもらっても大丈夫です。④からちょっと違います。
①90°-θの点はどこか
90°からθを引いた所の点ですよね。単位円上の点をy軸からθだけ時計回りに動かした点、上図だと点Cのことです。
②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る
点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形CODの2つの直角三角形ができましたね。
③合同な三角形を見つけよう
先ほど作った直角三角形は実は合同な三角形であり△OAB≡△CODとなります。
④今求めたい傾きと同じ値となる辺を探す
今回はtan(90°-θ)の値が知りたい。tan(90°-θ)は上図のOCの傾きですね。ですので、今回知りたい辺の長さはDCとODの長さです。△OAB≡△CODですので、DC=BO、OD=AB といえますね。
⑤ ④で見つけた辺の長さを求める
辺DCの長さは辺BOと、辺ODの長さは辺ABの長さと一致しているというのは④でわかりました。辺BOの長さは点Aのx座標の値と、辺ABの長さは点Aのy座標の値と一致してますので、BO=cosθ、AB=sinθ、よって DC=cosθ、OD=sinθとなります。
⑥ ⑤で見つけた値と今求めようとしている値を一致させる
今求めたいのはtan(90°-θ)の値であり、それは上図のOCの傾きのこと。
よってとなります。
tanもだいたい同じやり方でできましたね。
tanはもう1つ求め方がありまして、前の記事にも書いたと思いましたが
ですので、例えばtan(90°-θ)の値だったら、
と求めることもできます。tanは自分の好きな方で求めると良いかと思います。
ここまでで紹介した①〜⑥の手順で例題以外のパターンにも対応できると思います。
5)加法定理
図で考えるのが苦手だよー!!勘弁してくれーって思った人もいるかと思います。そんな人は加法定理で解いてしまいましょう。実際私も加法定理でやってた時期がありました。加法定理についての詳しい説明は次の記事で説明しようと思っていますので、すみませんが今回は割愛させてもらいます。
みたいな感じで解けます。
今回は (90°±θ)、(180°±θ)の話をさせてもらいました。基本は単位円で合同な三角形を使って考えます。元の角度と値を求めたい角度2つの三角形を書いて考えていきましょう。どうしても図が苦手な人は次の記事に説明する加法定理を使っていいと思います。今回の記事を読んで (90°±θ)、(180°±θ)関連の問題を克服してくれると嬉しいです。