医学生Gの数学ノート

スキマ時間で読める数学の記事を数学塾講師経験のあるメンバーがお届けします！

#12 余弦定理のうんちく

〜高1

　こんにちは、医学生Gです。中高生は夏休みが始まりウキウキしているところでしょうか。人と差をつけるなら夏休みが勝負ですね！ファイトです(^^)

　

　さてさて、本題の余弦定理の話をはじめようと思います。高校生の初めに習う余弦定理、 $a^2=b^2+c^2-2bccosA$ を暗記した人が多いかと思います。しかし、これは当たり前なことを式にしたもう一つの余弦定理から生まれた第２余弦定理だったのです。

　え？もう1つの余弦定理ってなんだよ！って思う方も少なくはないでしょうか。

　今回はそのもう一つの余弦定理である第一余弦定理と、第一余弦定理を用いた第二余弦定理の導き方をまとめました。1)~4)までありますので早速みていきましょう！

1)第一余弦定理

　先ほども述べたように第一余弦定理とは当たり前のことを式にしたものです。

f:id:sarugorirag:20190727003803p:plain

　上の図のような三角形があるとします。それぞれの頂点から対辺に垂線を下ろしてcosを考えることにより、各辺の長さを残りの辺の長さと角度を用いて表します。例として上の図では頂点Cから垂線を下ろしました。このときcをaとbを使って表すと $c=a \cosβ+b \cosα$ となります。これをa、bについても同じように考えると次のようになります。

$\begin{cases}a=b\cosγ+c\cosβ\cdots①\\b=c\cosα+a\cosγ\cdots②\\c=a\cosβ+b\cosα\cdots③\end{cases}$

上の式①〜③が第一余弦定理です。

2)第一余弦定理から第二余弦定理の導く

　さっき作った第一余弦定理①〜③を使っていつも見慣れている余弦定理である第二余弦定理を導きたいと思います。

　

　①×a-②×b-③×c より

$a^2-b^2-c^2=\underline{ab\cosγ}+\underline{ac\cosβ}-bc\cosα-\underline{ba\cosγ}-\underline{ca\cosβ}-cb\cosα$

＊下線部は消えます

整理すると

$a^2-b^2-c^2=-2bc\cosα$

$b^2$ と $c^2$ を右辺に移行して

$a^2=b^2+c^2-2bc\cosα$

いつものやつが出てきましたね。他の2つ同じやり方ですのでぜひ求めてみてください。

3)ベクトルを用いた余弦定理の証明

　ベクトルを使っても余弦定理を導くことができますので紹介します。

ベクトルをまだ知らない人はスルーしてもらってかまいません。

f:id:sarugorirag:20190727012803p:plain

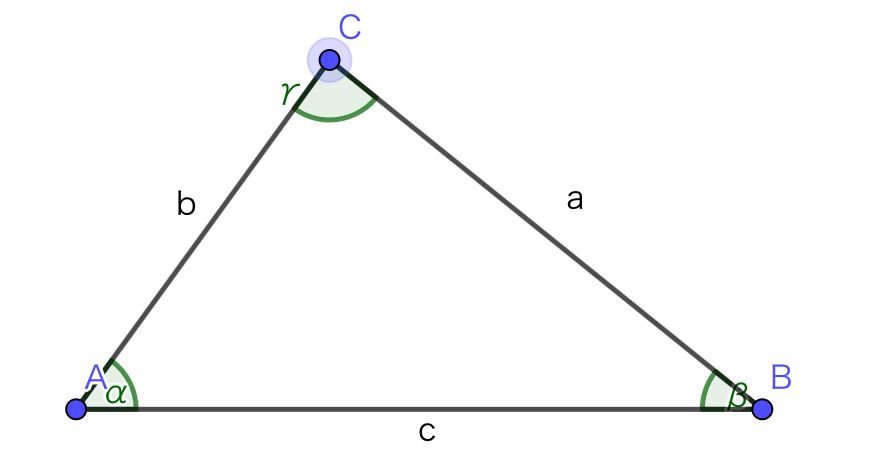
　上のような三角形があるとします。

${|\vec{CB}|}={|\vec{AB}-\vec{AC}|}$

ですので、両辺を二乗して

${|\vec{CB}|}^2={|\vec{AB}-\vec{AC}|}^2$

$={|\vec{AB}|}^2-2(\vec{AB}・\vec{AC})+{|\vec{AC}|}^2$

内積の部分をcosが登場する形に書き直すと

$={|\vec{AB}|}^2+{|\vec{AC}|}^2-2|\vec{AB}||\vec{AC}|\cosα$

これより

$a^2=b^2+c^2-2bc\cosα$

おなじみのやつが出てきましたね。これがベクトルでの証明です。

4)三平方の定理と余弦定理

ここで、余弦定理と三平方の定理の関係性についてお話ししたいと思います。

　余弦定理をやっていて中学校で習った三平方の定理が余弦定理の一部であったということに気づいていましたか？

余弦定理 $a^2=b^2+c^2-2bc\cosα$ において、αは0°から180°の間のどんな角度でも大丈夫ですが、ここにα=90°を代入してみてください。

$\cos90°=0$ ですので

$a^2=b^2+c^2$ となります。

これはまさしく三平方の定理そのものですよね。

　すなわち、余弦定理のうちα=90°という特別な場合(直角三角形となる場合)を考えるとそれは三平方の定理なのです。よって「余弦定理は三平方の定理を拡張したもの」とも考えることができますね。

　今回はみなさんが覚える余弦定理を原点から導き出す方法と、その他の余弦定理についてのお話をさせてもらいました。今回の記事で余弦定理について少しでも理解が深まってくれると嬉しいです。