医学生Gの数学ノート

スキマ時間で読める数学の記事を数学塾講師経験のあるメンバーがお届けします！

#13.5 tanのグラフはなぜ途切れるのか

深イイ話

最近、とある勉強熱心な方から

「tanのグラフはなぜ途切れるのか。

     tan90°についてどのように理解しておけば良いのか。」

という質問をいただきましたのでその回答をこの場で共有しておこうと思います。

 

1)三角関数の定義

まず大前提として今回の回答にあたっては、三角関数の定義は単位円を用いたものとします。

直角三角形を用いた定義では0<θ<90°の範囲に限られているのでθが90°になる瞬間について考えることができませんからね。

以下、記事#11の復習になりますが

f:id:sarugorirag:20190727115056p:plain

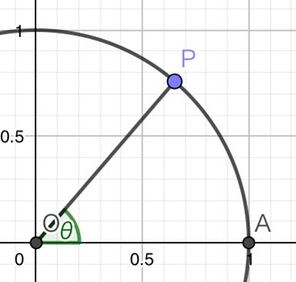
上の図において(1,0)を点A、単位円周上の点を点Pとし、\angle{AOP}=\theta と定めた時の点Pの座標を(sinθ,cosθ)とします。sin,cosを点Ｐの座標として定義することにより0<θ<90°の制限がなくなり、回し放題になるのでした。覚えていますか？

ここで、tan\theta=\frac{sin\theta}{cos\theta}ですが、直線OPの傾きも同じく\frac{sin\theta}{cos\theta}の値をとりますので、tanθは直線OPの傾きといえます。

 

 

2)傾きの定義から考える

 さて、 1) で「tanθは傾き」と述べましたが傾きの定義は覚えていますか？

中学で学ぶ内容ですが

(傾き)=\frac{(yの増加量)}{(xの増加量)}   というやつです。

一次函数 y=ax+bのaの部分が、傾きの値になっているんでしたよね。

 例えば次の図のような場合には

f:id:sarugorirag:20190814224826j:plain

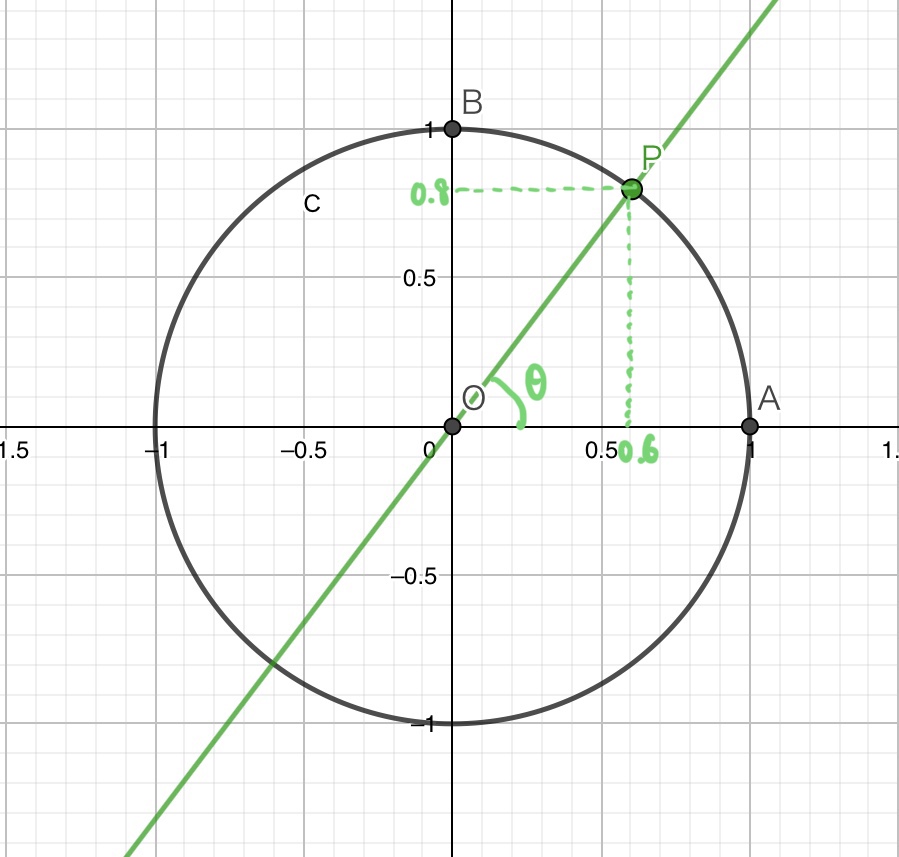
傾きは \frac{(yの増加量)}{(xの増加量)}\quad=\frac{0.8}{0.6}=\frac{4}{3} となります。


このように、”xの増加量”と”yの増加量”のふたつの値から傾きを計算できるわけですが、θが90°となる場合はどうでしょうか。次の図のような状態になっていますね。

f:id:sarugorirag:20190814230408j:plain

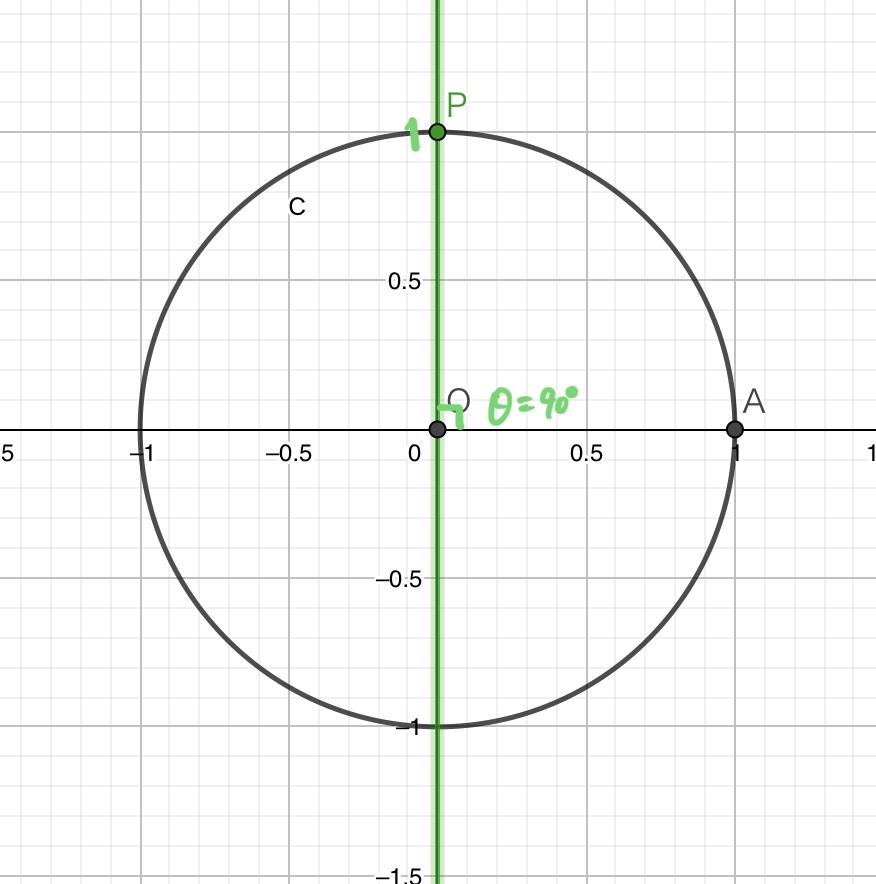
 気づきましたか？困りますよね。

 (傾き)=\frac{(yの増加量)}{(xの増加量)}    を計算しようとしても、xの増加量というやつがないんです。分母に入れる数字がない！困った！！

2点P,Oの間にx座標の差が少しでもあれば計算できるのですが、今回のように直線OPが完全な縦線になる場合にのみ、傾きは計算不能となります。

よってこのようなy軸と平行な直線(縦線)に対して、傾きは定義できないのです。「こーゆー縦線のとき、傾きは計算しないの！ (怒)」という約束になっているのですね。

 

ここまでのまとめ

θ=90°のとき、傾きは無し(定義外)。 そのためtanθの値もなし。

値なしの部分があるため、tanのグラフは途切れるのです。(下図)

f:id:sarugorirag:20190814232459j:plain

 

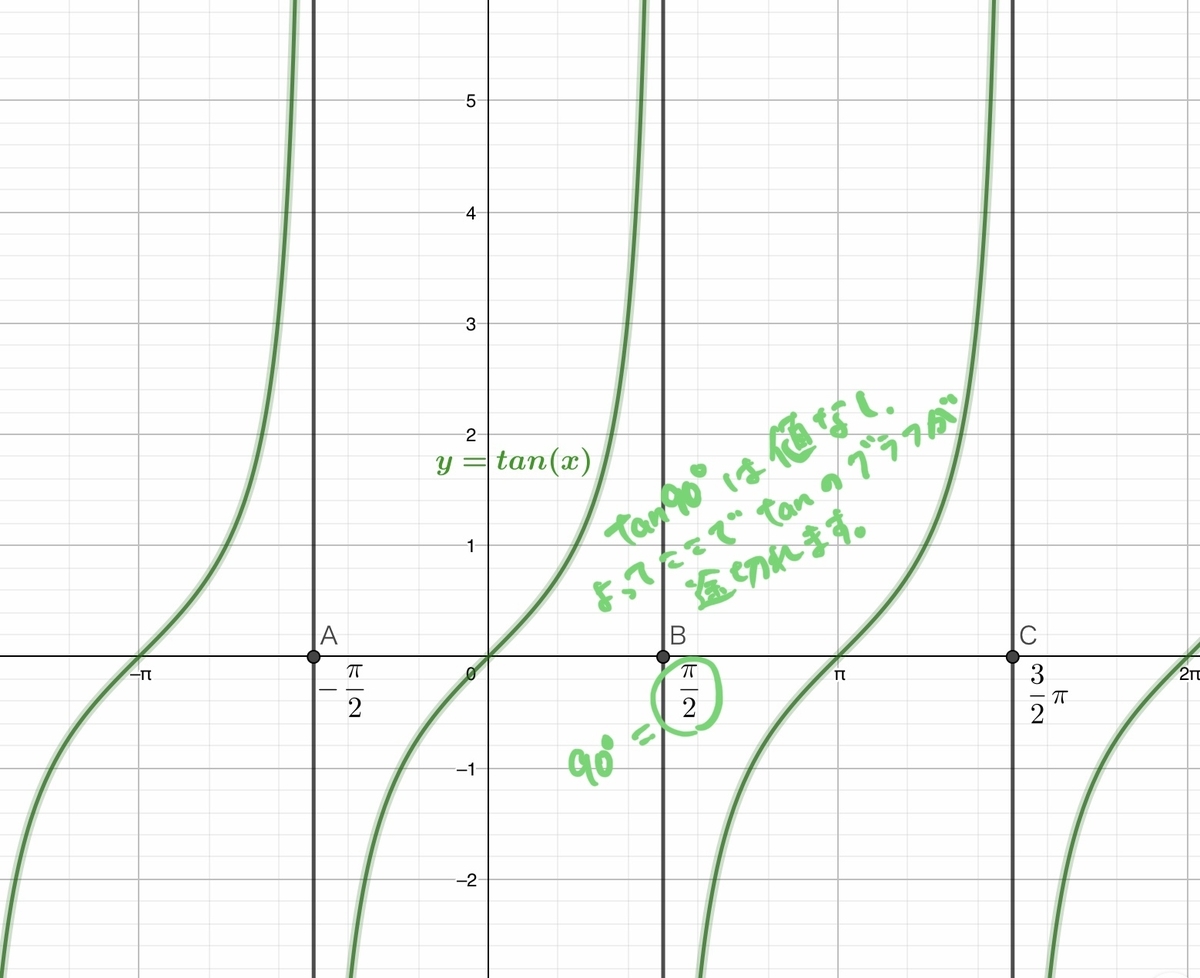
この説明で納得していただけたでしょうか？

納得できた方はここまでで終わってもらってオッケーです。

でも勘のいい人なら「xの増加量を0にして傾きの計算を強行すれば良い」と考えることでしょう。そんな方への説明をこれからしていきます。

少し踏み込んで、「極限」の考え方が登場します。準備はいいですか？

 

 

3)極限を用いた考え方

xの増加量を0として、計算を強行してみましょう。

O(0,0) P(0,1) ですので

\frac{(yの増加量)}{(xの増加量)}\quad=\frac{1}{0}

分母が0の分数が出てきました。なんだコイツは って感じですよね。

それもそのはず。こんな数字はないんです。0をいくつ合わせても1にはなりませんからね。そこで、極限という考え方で、それっぽい答えを探しにいきます。

\frac{1}{1}をスタートにして分母をどんどん小さくしていき、0に近づけていきます。

\frac{1}{1}=1

\frac{1}{0.1}=\frac{10}{1}=10

\frac{1}{0.01}=\frac{100}{1}=100

\frac{1}{0.001}=\frac{1000}{1}=1000

分母が0に近づくほど数が大きくなっていくのがわかりますか？

このノリで、「分母が0になるときには限りなく大きい数になるのだろう」

と考え、「 ∞:無限大 」という記号を使うわけです。

※実際にtanのグラフをみると、90°手前で曲線がぐんぐん上へ伸びていきます。この部分が限りなく大きい数になっていく様子を表しています。

 

 

では話を戻しましょう。

tan90°=(直線OPの傾き)=\frac{(yの増加量)}{(xの増加量)}\quad=\frac{1}{0}=\infty

で良いでしょうか？

 

答えはNoです。

“傾き\frac{4}{3}”と”傾き∞ “との間で決定的に違うことがあります。 

それは「値が定まっているか」という点です。

ちゃんと目盛りが打ってある数直線上において、\frac{4}{3}という数字は ここ！

と指させるのに対し ∞は無理ですよね。数直線をどこまで延長しても ここ！ とは言えないのです。

f:id:sarugorirag:20190815104559j:plain

 傾きとは直線の状態をを表現する尺度であり、それを用いて他の数値を計算したりします。そんな数値が、数直線上で指させないようなぼんやりとしたものではいけません。よって、tan90°の値は「無し」ということになるのです。

 

tan90°の値が決まらないということをもう少しお話ししましょう。

先ほど分母をどんどん小さくしていってtan90°としたときは分母分子共に正の数でしたから、90°より小さい角度の方から87°,88°,89°…と90°に近づけたわけですが(下図の赤文字)

f:id:sarugorirag:20190815111330j:plain

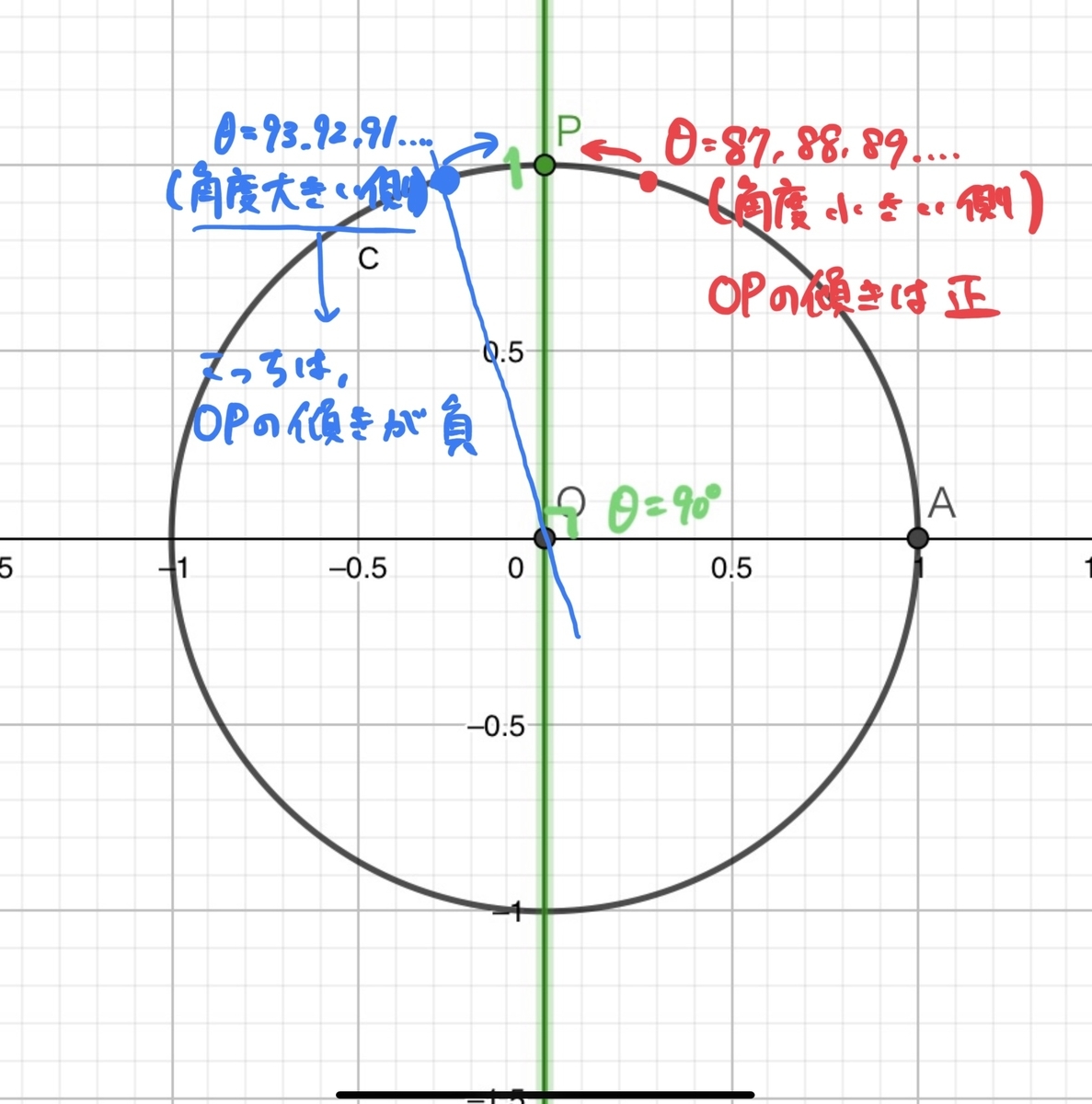
青文字のように逆サイド(90°より大きい角度のほう)から90°に近づくこともできるはずです。この場合、傾きは負の数となっていることに注意してください。するとこちら側では93°,92°,91°…と90°に近づくに連れて傾きが限りなく小さな値になっていくのがわかりますか？

式にするとこうなります。

赤: \displaystyle \lim_{\theta\to90°-0}tan(\theta)=\infty

  (訳:θを90°より小さい側から90°に近づけると、tanθは限りなく大きい値になります)

青: \displaystyle \lim_{\theta\to90°+0}tan(\theta)=-\infty  
  (訳:θを90°より大きい側から90°に近づけると、tanθは限りなく小さい値になります)

 

どちらもtan90°の値を求めようとしているのに、片方は∞、もう片方は-∞と真逆の結果になっています。変ですよね。このことからも、tan90°の値は定まらないということを感じてもらえると嬉しいです。

 

 

ついつい話が難しくなってしまいましたが、要するに「tan90°はとてもややこしいので考えないようにしましょう」ということです。

結局そんだけかい！と思うかもしれませんが「なぜ考えないのか」という部分、今回の記事の内容を知っておくことに意味があるのではないかと思う医学生Gでした(^^)