＃15 加法定理 その２ 遊んで加法定理を理解しよう！

　前回、加法定理を単位円で証明しましたけれども、ちゃんと理解できましたか？

今回は加法定理を長方形を使って証明しようと思います。

角度が限定されてしまうため、完璧な証明とは言えないのですが、遊びだと思って付き合ってください。

　後半は#13でやった90°+θを加法定理を使って実際に出してみようと思いますので、最後まで読んでみてください。

1)長方形を使ったお遊び！

　加法定理、長方形を使って証明する方法を知ってましたか。結構面白いですのでみていきましょう。

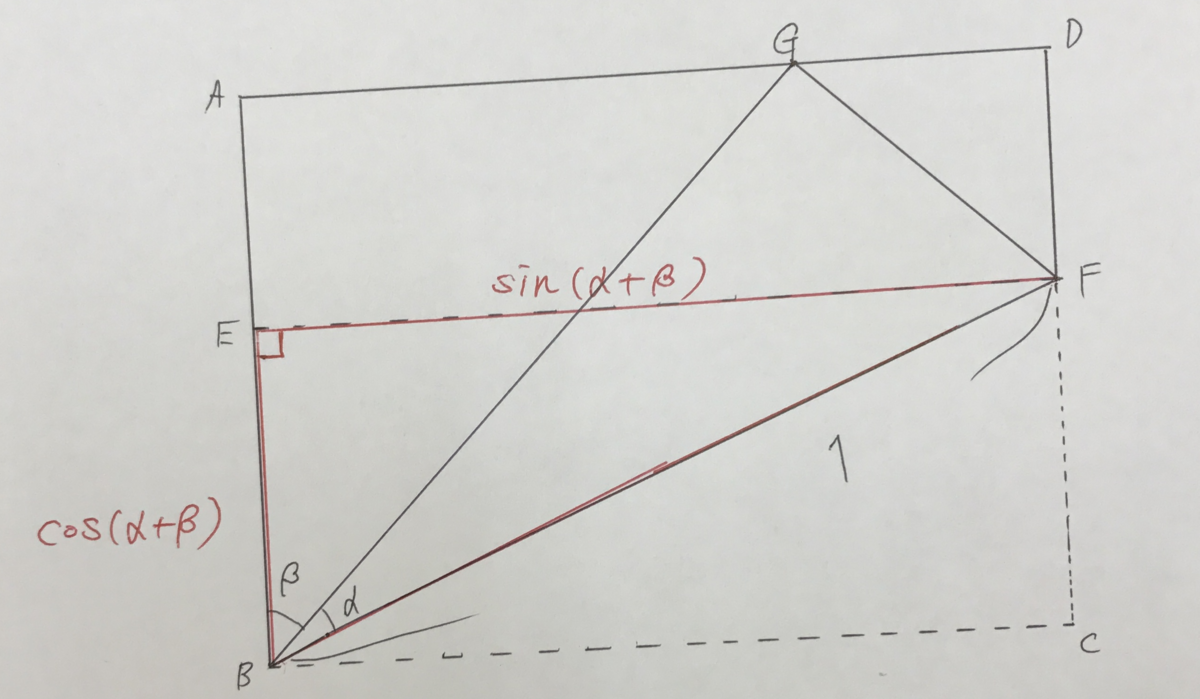
　ちょっと斜めになってしまって申し訳ないんですが、上図のように点Cを点Gのところまで長方形を折り曲げます。そしてBF=1、、と設定します。

　こうするとになります。ここで上図の赤い三角形である△FBEに注目してください。BF=1ですので、sin、cosを取るとEF=sin(α+β)、EB=cos(α+β)になりますね。

　とりあえず、sin(α+β)がEFの長さ、cos(α+β)がEBの長さなのを覚えておいてください。以下はこのEF、EBの長さをα、βを用いて求めていきます。

 　次に、注目する三角形を変えましょう。上の図の青い三角形である△GBFに注目しましょう。

でBF＝１ですので、△GBFで同じようにsin、cosを取るとGF=sinα、GB=cosαになります。

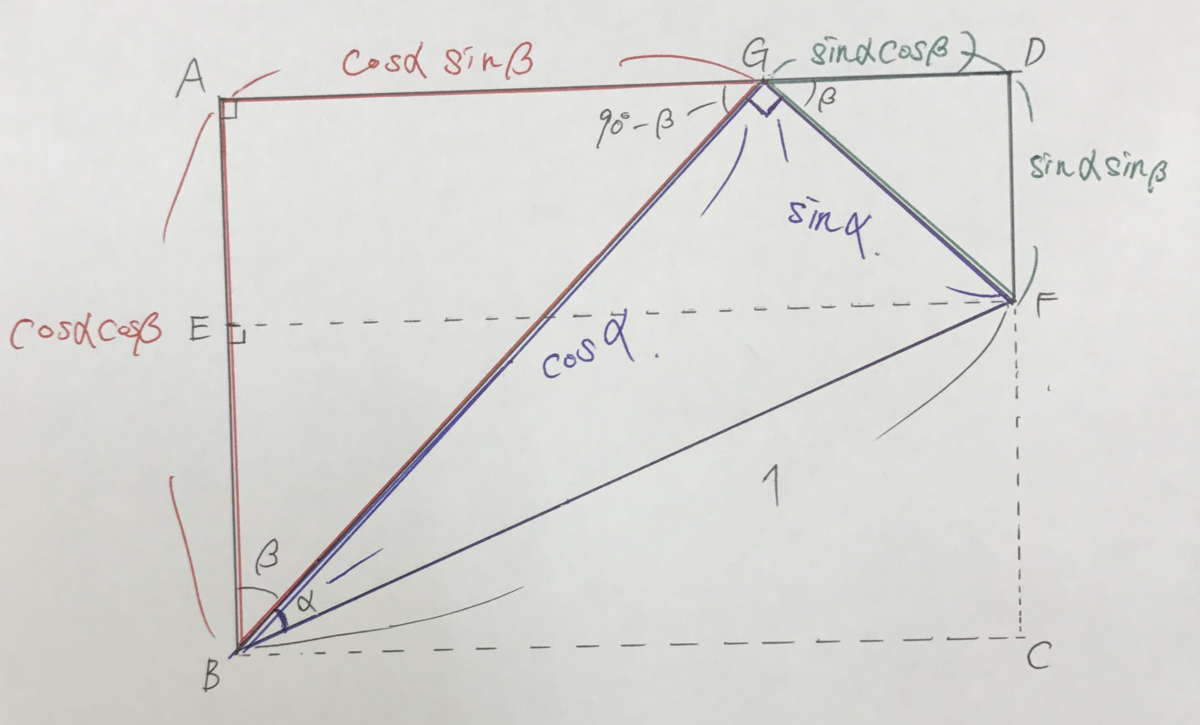
　GF=sinα、GB=cosαを前の画像のところで求めました。

そしたら、まずはGF=sinαを含む三角形から見ていきましょう。

　GFを含む三角形は△GFDで上の図の右上の緑色の三角形です。

上図のように、ですので、

になります。

そうするとGF=sinαだから残りの辺の長さGD=sinαcosβ、DF=sinαsinβになりますね。

 この２辺は最初のEF、EBを求めるのに必要です。

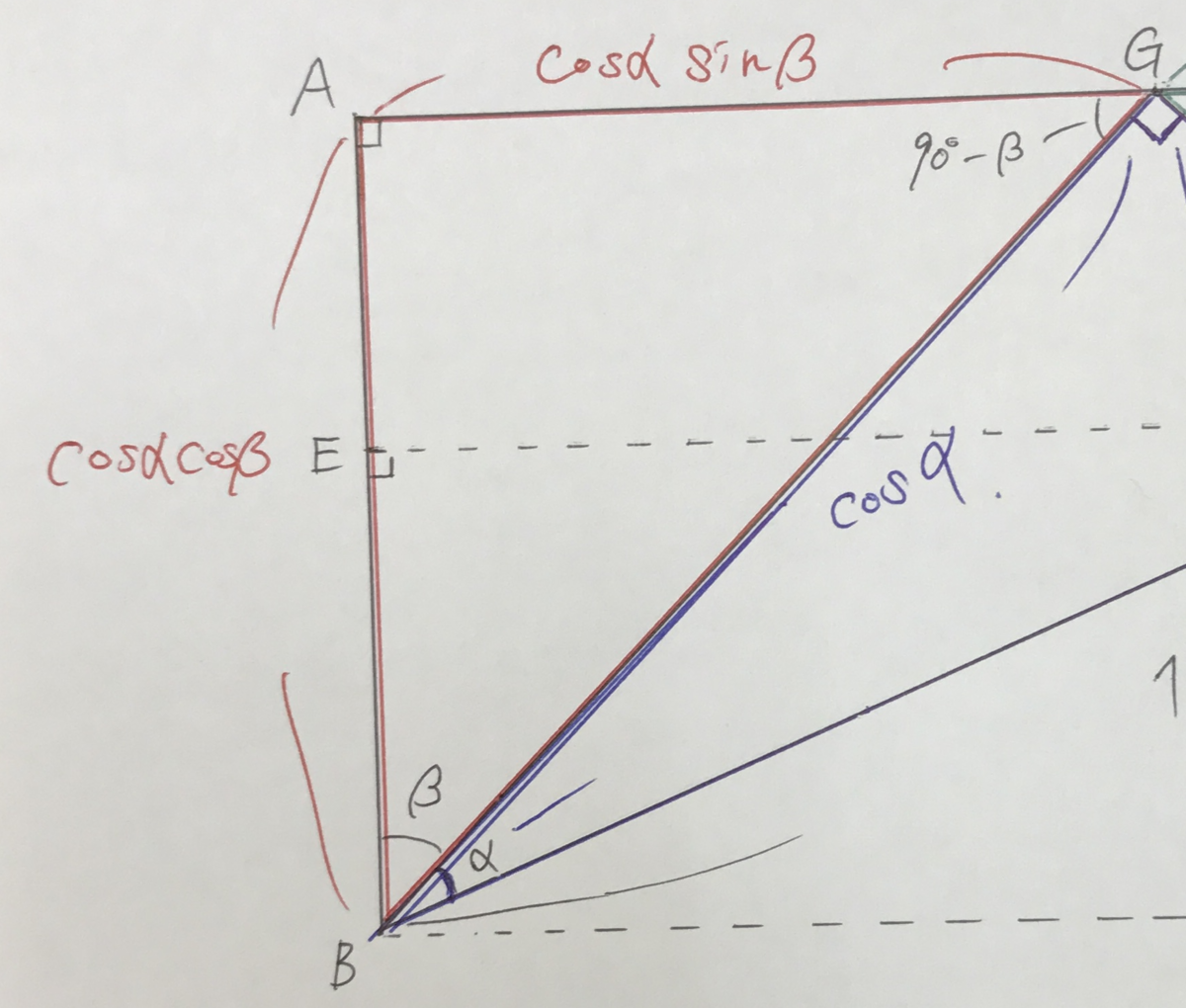
次に、GB=cosαを含む三角形である△GBAについて見てみよう。

GB=cosα、 ですので、これも残りの辺の長さを求めていきましょう。これも、sin、cosを取るとAG=cosαsinβ、AB=cosαcosβになりますね。

 この２辺もEF、EBの辺を求めるのに必要です。

ここまでの話は理解できましたか？そしたら今まで求めてきた辺を使ってsin(α+β)、cos(α+β)であるEF、EBを求めていきましょう。

上の図を参考にして見ていきましょう。

EFの長さは長方形の上辺であるAGとGDを足した長さですね。また、EBの長さはABからAE(=DF)を引いた長さに一致しますね。これを実際に長さを代入して求めていきます。

すると、

EF=sin(α+β)=AG+GD=cosαsinβ+sinαcosβ

EB=cos(α+β)=AB-DF=cosαcosβ-sinαsinβ

　出てきましたね、sin(α+β)、cos(α+β)が。こんな感じで長方形を用いて加法定理を導出することができます。

　最初にも言いましたが、この求め方は角度が限定されているため、証明には使えませんが、雑学として覚えておくといいかなと思います。

2)加法定理を使って90°+θのやつを求める

　#13でやった90°+θのやつを実際に加法定理を用いてsin(90°+θ)、cos(90°+θ)を求めてみましょう。

sin(α+β)=cosαsinβ+sinαcosβ

cos(α+β)=cosαcosβ-sinαsinβ

実際にα=90°、β=θを代入してやってみましょう。

sin(90°+θ)

=cos90°sinθ+sin90°cosθ

=cosθ

＊cos90°=0、sin90°=1

cos(90°+θ)

=cos90°cosθ-sin90°sinθ

=-sinθ

　図を描くのが苦手な人は加法定理を使って求めるのもいいと思います。sin、cosのどちらかが0になりますので、簡単に求めることができます。ちなみに私は加法定理で頭の中でやってました（笑）。

　今回は長方形を使った加法定理の証明と実際に加法定理を使ってsin(90°+θ)、cos(90°+θ)を求めてみました。長方形の方はお遊びですので、加法定理の証明問題がでてきたら書かないように気をつけましょう。まぁ、もし単位円が思いつかなかったら書いてみるのもアリだとは思いますが（笑）。90°+θのやつは図を書いてもよし、加法定理で求めてもよしですので、自分に合う方法でやるのがいいと思います。今回の記事を読んで数学をより深く理解してもらえると嬉しいです。

いろんな考え方を知っておくということが難関大数学に立ち向かう上で強みになると思いますよ。(^^)