2019-08-05

#12 余弦定理のうんちく

〜高1

　こんにちは、医学生Gです。中高生は夏休みが始まりウキウキしているところでしょうか。人と差をつけるなら夏休みが勝負ですね！ファイトです(^^)

　さてさて、本題の余弦定理の話をはじめようと思います。高校生の初めに習う余弦定理、 $a^2=b^2+c^2-2bccosA$ を暗記した人が多いかと思います。しかし、これは当たり前なことを式にしたもう一つの余弦定理から生まれた第２余弦定理だったのです。

　え？もう1つの余弦定理ってなんだよ！って思う方も少なくはないでしょうか。

　今回はそのもう一つの余弦定理である第一余弦定理と、第一余弦定理を用いた第二余弦定理の導き方をまとめました。1)~4)までありますので早速みていきましょう！

1)第一余弦定理

　先ほども述べたように第一余弦定理とは当たり前のことを式にしたものです。

f:id:sarugorirag:20190727003803p:plain

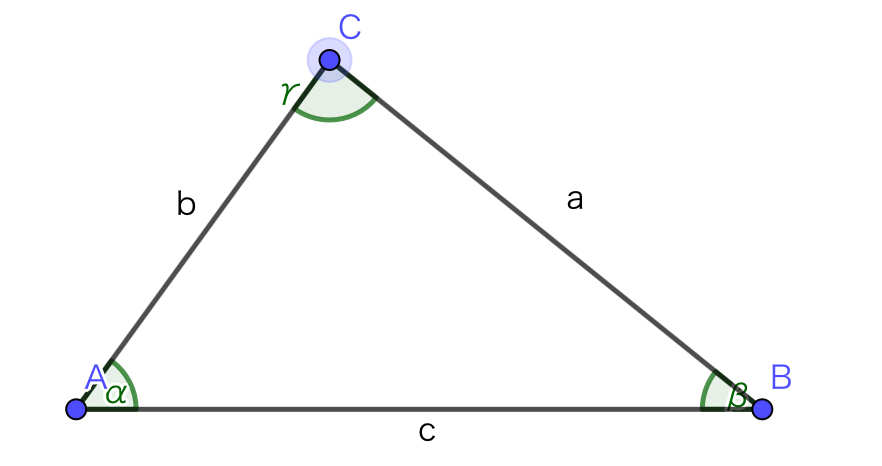
　上の図のような三角形があるとします。それぞれの頂点から対辺に垂線を下ろしてcosを考えることにより、各辺の長さを残りの辺の長さと角度を用いて表します。例として上の図では頂点Cから垂線を下ろしました。このときcをaとbを使って表すと $c=a \cosβ+b \cosα$ となります。これをa、bについても同じように考えると次のようになります。

$\begin{cases}a=b\cosγ+c\cosβ\cdots①\\b=c\cosα+a\cosγ\cdots②\\c=a\cosβ+b\cosα\cdots③\end{cases}$

上の式①〜③が第一余弦定理です。

2)第一余弦定理から第二余弦定理の導く

　さっき作った第一余弦定理①〜③を使っていつも見慣れている余弦定理である第二余弦定理を導きたいと思います。

　①×a-②×b-③×c より

$a^2-b^2-c^2=\underline{ab\cosγ}+\underline{ac\cosβ}-bc\cosα-\underline{ba\cosγ}-\underline{ca\cosβ}-cb\cosα$

＊下線部は消えます

整理すると

$a^2-b^2-c^2=-2bc\cosα$

$b^2$ と $c^2$ を右辺に移行して

$a^2=b^2+c^2-2bc\cosα$

いつものやつが出てきましたね。他の2つ同じやり方ですのでぜひ求めてみてください。

3)ベクトルを用いた余弦定理の証明

　ベクトルを使っても余弦定理を導くことができますので紹介します。

ベクトルをまだ知らない人はスルーしてもらってかまいません。

f:id:sarugorirag:20190727012803p:plain

　上のような三角形があるとします。

${|\vec{CB}|}={|\vec{AB}-\vec{AC}|}$

ですので、両辺を二乗して

${|\vec{CB}|}^2={|\vec{AB}-\vec{AC}|}^2$

$={|\vec{AB}|}^2-2(\vec{AB}・\vec{AC})+{|\vec{AC}|}^2$

内積の部分をcosが登場する形に書き直すと

$={|\vec{AB}|}^2+{|\vec{AC}|}^2-2|\vec{AB}||\vec{AC}|\cosα$

これより

$a^2=b^2+c^2-2bc\cosα$

おなじみのやつが出てきましたね。これがベクトルでの証明です。

4)三平方の定理と余弦定理

ここで、余弦定理と三平方の定理の関係性についてお話ししたいと思います。

　余弦定理をやっていて中学校で習った三平方の定理が余弦定理の一部であったということに気づいていましたか？

余弦定理 $a^2=b^2+c^2-2bc\cosα$ において、αは0°から180°の間のどんな角度でも大丈夫ですが、ここにα=90°を代入してみてください。

$\cos90°=0$ ですので

$a^2=b^2+c^2$ となります。

これはまさしく三平方の定理そのものですよね。

　すなわち、余弦定理のうちα=90°という特別な場合(直角三角形となる場合)を考えるとそれは三平方の定理なのです。よって「余弦定理は三平方の定理を拡張したもの」とも考えることができますね。

　今回はみなさんが覚える余弦定理を原点から導き出す方法と、その他の余弦定理についてのお話をさせてもらいました。今回の記事で余弦定理について少しでも理解が深まってくれると嬉しいです。

2019-07-31

#11 sin、cosの定義が面白い！

〜高1

　高校1年生で初めてsin、cosを勉強すると、難しい数式扱ってる気分になってワクワクするものですよね。まあ、もしかしたら意味不明なやつが出てきてやりたくないーって思ってしまう人もいるかもしれませんが（笑）

　ところでsin、cosの話の序盤は理解できるのに、単位円が出てきた途端「もう無理！」って言う人はいませんか？今回はそんな人に向けた記事です。

　今回の要点を先にお伝えすると、sin,cosの定義は段階的に変化するということです。単位円が登場するタイミングで定義が変化するため、そこでつまずく人が多いのです。これをふまえた上で以下の話を読んでみてください。これから順に説明する1)、2)の定義は、同じではありません。それでは、どのように変化するかをチェックしてくださいね。

1)直角三角形を用いた定義

sin,cosとの初めての出会い…

数学1の図形と計量の単元ではまず直角三角形を用いた定義が登場します。

f:id:sarugorirag:20190721155911p:plain

上の図のように直角三角形ABCがあるとします。

$\angle{ACB}=\theta$ とすると、 $sin \theta=\frac{c}{b},cos\theta=\frac{a}{b},tan\theta=\frac{c}{a}=\frac{sin \theta}{cos\theta}$ と定義します。

※覚え方

上の図のように筆記体のs、c、tの書き始めの方が分母になり、書き終わりの方が分子になります。

　＊sの場合は書き始めが斜辺AC、書き終わりがABですので、 $sin \theta=\frac{c}{b}$ です。

　この定義では、θを直角三角形の一つの角度として設定していますので、 $0＜\theta＜\frac{π}{2}$ の範囲での定義になります。

　しかし、欲張りな人は言いました。「これではθの範囲がせまい。 $0＜\theta＜\frac{π}{2}$ の範囲外の角度についても、sin、cosの値を考えたい」

そんな願いを叶えるために登場するのが次の、単位円による定義なのです。

2)単位円を用いた定義

f:id:sarugorirag:20190727115056p:plain

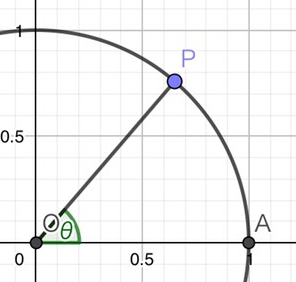
　上の図のような半径1の単位円において、点Aを座標(1,0)、点Pを単位円周上の点で、 $\angle{POA}=\theta$ として、この時の点Pの座標を(cosθ,sinθ)と定義します。つまりこのとき、sin,cos を辺の比ではなく点Ｐの座標として定義したわけです。

※この時のθは点Pと点Aが重なる時を0として、点Ｐを反時計回りに移動するとθの値は正の数として増加し、時計回りに動かすとマイナスになります。

　この定義ならθは何度まで回すことができますか？

θを二週目、三週目…と回すことによって2πを超える角度だってsin,cosの値が得られます。つまり回し放題！ $0＜\theta＜\frac{π}{2}$ の範囲に限定されず、θはどんなに大きくても、小さくても大丈夫。

定義1)では $0＜\theta＜\frac{π}{2}$ に限られていたθが、定義2)になると角度の制限がなくなりました。角度θを制限から解放すること。これこそが定義を変える理由なのです。

さて、同じsin cos について1)と2)の異なる定義が登場しましたが、ここからはこれら２つの定義の関係性を見ていきましょう。

定義1)で求めたsin60°の値と定義2)で求めたsin60°の値が違ったりしたら困りますよね？その点をチェックしていきます。

f:id:sarugorirag:20190722150048p:plain

上図のように点Pからx軸に下ろした垂線の足を点Hとします。

　単位円を用いた定義２では点Pの座標は(cosθ,sinθ)ですので、OH=cosθ、PH=sinθになりますね。

　直角三角形を用いた定義１では $cos\theta=\frac{OH}{OP}=\frac{OH}{1}=OH$ 、 $sin\theta=\frac{PH}{OP}=\frac{PH}{1}=PH$ となります。

　定義１でも定義２でもcosθ=OH、sinθ=PH となっていますので、sin、cosの値は同じと言えます。つまり、 $0＜\theta＜\frac{π}{2}$ の範囲においては定義1)で考えても定義2)で考えてもsin,cosの値は同じになるのです。当たり前に思うかもしれませんが、これはかなり大事なこと。これで、安心して使えますね(^^)

＊sin,cosが一致するということは $\frac{sinθ}{cosθ}$ の値をとるtanも一致しています。

　定義の変化に気づかずに定義１のまま単位円に突入してしまうので、わからなくなってしまうのです。単位円が出てくるタイミングでsin,cosは再定義され、 $0＜\theta＜\frac{π}{2}$ の制限から解放される。「定義１と定義２は違う」ということを理解してもらえましたか？

＊ちなみに大学レベルではθをさらに複素数の範囲まで解放するため、また別の定義が追加されます。

　三角関数マスターになるための第一歩として、sin,cosの定義をしっかりと理解してもらえると嬉しいです。

2019-07-18

#10 因数分解の基礎　part2

〜高1

　今回の記事は前回に引き続き因数分解のお話をしていこうと思います。今回はより難しい因数分解を行う際のポイントをいくつか紹介していますので、3)〜5)をしっかりと読み込んでもらえると嬉しいです。それでは見ていきましょう。

3)困った時の打開策

#9の 2)因数分解の基本的な手順で上手くいかない場合に、 $a^2-b^2$ の形を目指して無理やり二乗を作ることによって解決する場合がありますので、その例とともに説明します。

例） $x^4+4$

「これどうやって因数分解するんだろう」って思いませんか？

こんな時に先ほど説明した $a^2-b^2$ の形を目指して無理やり二乗を作る方法をやってみます。

$x^4+4=(x^4+4x^2+4)-4x^2$

2乗を作るのに足りなかった $4x^2$ を補い、後ろで調整します。計算したら元の式に戻るように調整してくださ。

すると、

$x^4+4=(x^4+4x^2+4)-4x^2$

$={(x^2+2)}^2-{(2x^2)}^2=(x^2+2x+2)(x^2-2x+2)$

　上のように $a^2-b^2$ が作れたら、あとは $a^2-b^2$ の因数分解をして終わりです。

4)対称性のある式の扱い

　#9の 2)④で降べきの順に並べるとき、どの文字について降べきの順で並べるべきかをあらかじめ決めておきましょう。今回はaについての降べきの順にしてやっています。

あまりに対称的な式だとどの文字にするか迷ってしまうかもしれませんが、どれでもいいんです。1文字選んでそれに注目することが重要です。

例） $a{(b-a)}^2+b{(c-a)}^2+c{(a-b)}^2+8abc$

$=a{(b-a)}^2+b(c^2-2ac+a^2)+c(a^2-2ab+b^2)+8abc$

　　＊文字aを含むところを適宜展開しました。

$=(b+c)a^2+\{{(b-c)}^2+4bc\}a+(bc^2+b^2c)$

$=(b+c)a^2+(b^2-2bc+c^2+4bc)a+bc(b+c)$

$=\underline{(b+c)}a^2+{\underline{(b+c)}}^2a+bc\underline{(b+c)}$

＊共通因数 $(b+c)$ でくくります。

$=\underline{(b+c)}\{a^2+(b+c)a+bc\}$

$=(b+c)(a+b)(a+c)$

$=(a+b)(b+c)(c+a)$

　このように、1文字選んでしまえばごちゃごちゃせずに解くことができますので、ぜひ参考にしてみてください。

5)実際の入試問題

　それではこれまでの説明を踏まえて、実際の入試問題を解いてみましょう。

最初は自分でやってみてから解答を参考にしてみてください。

問題） $a^4+b^4+c^4-2a^2b^2-2a^2c^2-2b^2c^2$

それでは解答を書いていきたいと思います。解答の後に解説していきます。

$a^4+b^4+c^4-2a^2b^2-2a^2c^2-2b^2c^2$

$=a^4-2(b^2+c^2)+b^4+c^4-2b^2c^2$

$=a^4-2(b^2+c^2)a^2+{(b^2+c^2)}^2-4b^2c^2$

$={\{a^2-(b^2+c^2)\}}^2-{(2bc)}^2$

$=\{a^2-(b^2+c^2)-2bc\}\{a^2-(b^2+c^2)+2bc\}$

$=\{a^2-(b^2+2bc+c^2)\}\{a^2-(b^2-2bc+c^2)\}$

$=\{a^2-{(b+c)}^2\}\{a^2-{(b-c)}^2\}$

$=(a-b-c)(a+b+c)(a-b+c)(a+b-c){\cdots}$ 答

＊横浜市立大学2011

どうでしたか？できていましたか？

できなかった人のために解説していきます。

　まず、問題は対称性のある式ですのでaについての降べきの順に並べてやっていきたいと思います。

$a^4+b^4+c^4-2a^2b^2-2a^2c^2-2b^2c^2$ をaについて並べると

$=a^4-2(b^2+c^2)+b^4+c^4-2b^2c^2$ となります。

ここからが問題です。

因数分解できるじゃん！っと思って

$a^4-2(b^2+c^2)a^2+{(b^2-c^2)}^2$ としてしまうとこれ以上何もできなくなってしまいます。

　では、どう考えればいいかと言いますと、この式をよく見てみてください。 $\underline{{(b^2-c^2)}^2}$ が $\underline{{(b^2+c^2)}^2}$ だったら ${(x+y)}^2$ の形に因数分解できますよね？

　では ${(b^2+c^2)}^2$ なるようにしていきましょう！

　式全体に $\underline{+2b^2c^2}$ を足して最後で $\underline{-2b^2c^2}$ を引いて調節します。

すると、こうなります。

$=a^4-2(b^2+c^2)+b^4\underline{+2b^2c^2}+c^4-2b^2c^2\underline{-2b^2c^2}$

これを整理すると、

$=\underline{a^4-2(b^2+c^2)a^2+{(b^2+c^2)}^2}-4b^2c^2$

上記の式の下線部は ${(x-y)}^2$ の形に因数分解できますね。また、 $4b^2c^2$ は ${(2bc)}^2$ の形にできますのでやっていきましょう。

$={\{a^2-(b^2+c^2)\}}^2-{(2bc)}^2$

これは $x^2-y^2$ の形ですね。さらに因数分解していきます。

$=\{a^2-\underline{(b^2+c^2)-2bc}\}\{a^2-\underline{(b^2+c^2)+2bc}\}$

上の式の下線部の部分を-でくくります。

$=\{a^2-(b^2+2bc+c^2)\}\{a^2-(b^2-2bc+c^2)\}$

すると、また ${(x+y)}^2$ 、 ${(x-y)}^2$ の形で因数分解できますね。やっていきましょう。

因数分解するとこうなります。

$=\{a^2-{(b+c)}^2\}\{a^2-{(b-c)}^2\}$

また、 $x^2-y^2$ の形が出てきましたね（笑）

もう一度 $x^2-y^2$ の因数分解すると答えが出てきます。

$=(a-b-c)(a+b+c)(a-b+c)(a+b-c){\cdots}$ 答

どうでしょうか。理解できましたか？

　私はいつもこんな感じで考えて因数分解の問題を解いていますので、しっかりと押さえればある程度の問題は解けるようになると思います。

　今回は前回に引き続き因数分解についてお話ししていきました。今回の記事を読んでもらうことにより、以前は解けなかった問題も少しは解けるようになっていると思います。#9も合わせて因数分解の話を読んで、少しでも多くの問題が解けるようになってもらえると嬉しいです。

2019-07-15

#9 因数分解の基礎　part1

〜高1

　今回の記事では因数分解のコツをお伝えしようと思います。入試問題になってくると#8の記事で説明した計算と今回の記事で説明する因数分解は出来て当たり前になってきますので、まず基本的なことである1)と2)をしっかりと理解してくださいね。

1)展開の逆をせよ！

(整数の積)＝(単項式の和) のとき、例えば $(x+2)(2x-1)=2x^2+3x-2$

(左辺)→(右辺)の変形を"展開"、

逆に、(右辺)→(左辺)の変形を"因数分解"といいます。

　つまり、因数分解とは展開の逆の操作であり、基本的にこれまでの展開公式を逆方向に使えばいいのです。

例） $a^2+2ab+b^2={(a+b)}^2$

　　 $a^2-b^2=(a+b)(a-b)$

因数分解がどんなものなのか理解できましたでしょうか。

2)因数分解の基本的な手順

因数分解は基本的に次のような手順でするといいと思います。

$\begin{cases}①実は公式そのまんまじゃないかチェック\\②共通因数をくくり出す\\③グループ化\\④降べきの順に並べる\\⑤たすき掛けor展開公式の逆\end{cases}\$

①〜⑤を $4zy-30z-4zx+2z{(x-y)}^2$ を例に使って説明していきます。

①実は公式そのまんまじゃないかチェック

$4zy-30z-4zx+2z{(x-y)}^2$ ←これは違いますね。

＊ $a^2+4ab+4b^2$ などは公式がそのまま使えるので一撃でいきます。

②共通因数をくくり出す

共通因数"2z"がありますのでくくり出します。

$4zy-30z-4zx+2z{(x-y)}^2=2z \{2y-15-2x+{(x-y)}^2\}$

③グループ化

　{ }の中の $2y-2x$ を-2でくくると $(x-y)$ が出てきますね。これで{ }の中は $\underline{(x-y)}$ でグループ化できているのがわかりますでしょうか。

$2z\{2y-15-2x+{(x-y)}^2\}=2z\{-2\underline{(x-y)}-15+{\underline{(x-y)}}^2\}$

④降べきの順に並べる

　③の過程で{ }の中がグループ化できましたので、今度はグループ化した $(x-y)$ についての降べきの順に並べましょう。

$2z\{{\underline{(x-y)}}^2-2\underline{(x-y)}-15\}$

⑤たすき掛けor展開公式の逆

　{ }の中は因数分解できますか?

かけて-15、足して-2の組み合わせです。-5と3がありますね。これで{ }の中を因数分解してみましょう。

$2z\{{(x-y)}^2-2(x-y)-15\}=2z\{(x-y)-5\}\{(x-y)+3\}$

　もしわかりにくかったら $(x-y)=A$ などと置いてみるといいと思います。

$(x-y)=A$ とすると

$2z\{{(x-y)}^2-2(x-y)-15\}$

$=2z\{A^2-2A-15\}$

$=2z\{A-5\}\{A+3\}$

$=2z\{(x-y)-5\}\{(x-y)+3\}$

＊Aは自分が勝手においた文字ですので最後は元に戻しましょう。

①〜⑤をまとめるとこんな感じです。

$4zy-30z-4zx+2z{(x-y)}^2$

$=2z \{2y-15-2x+{(x-y)}^2\}$

$=2z\{-2\underline{(x-y)}-15+{\underline{(x-y)}}^2\}$

$=2z\{{\underline{(x-y)}}^2-2\underline{(x-y)}-15\}$

$=2z\{(x-y)-5\}\{(x-y)+3\}$

　式の次数が高いと、公式など種々のテクニックが使いにくくなることが多いですので、文字の種類が複数ある場合は次数の低い文字について整理してみるといいと思います。難しい式になると、①から⑤のサイクルを何度かくり返して解くこともあります。

ここで１つポイントを述べておきますが、

「④降べきの順に並べる」を甘くみてはいけません。

その後公式を使ったり、たすき掛けをしたりすることになると思います。公式は普通降べきの順に並んだ形で覚えるでしょうし、たすき掛けも、2次→1次→定数項と降べきの順に並べてから行うのが一般的です。だから、降べきの順に並び替えるということは、⑤たすき掛けor展開公式の逆 を正確に行うために必須の準備と言えます。

　今回は因数分解の基本的なやり方を説明しました。次回は難しい因数分解の対処法について説明していきますので、この記事を理解してもらって次回も読んでもらえると嬉しいです。

2019-07-12

#8 演算基礎

〜高1

　今回は高校レベルの数式を扱うに当あたっての基本的なポイントをいくつか紹介したいと思います。

超初心者向けに丁寧に書きましたので、計算ミスが目立つ人や計算が遅いな〜と思う人はぜひ参考にしてみてください。

1)指数法則

① $x^a×x^b=x^{a+b}$ $x$ が合わせて何回かけられているかな？　

今回の場合はa+b回かけられていますので、 $x^{a+b}$ になりますよね。2が3回かけられていたら $2^3$ になるのと同じです。

例） $2^3×2^4=2^{3+4}=2^7$ 今回は2が合計で7回かけられていますので $2^7$ になります。　

② ${(x^a)}^b=x^{ab}$ これは $\underbrace{x^a×x^a×{\cdots}×x^a}_{x^aがb個}$ となっているため $x^a$ がb回かけられていますよね。よって①を利用すると $x^{\overbrace{a+a+{\cdots}+a}^{b個}}$ で、 $a$ が $b$ 個あるので $x^{ab}$ になります。

例) ${(2^3)}^4=2^{\overbrace{3+3+3+3}^{4個}}=2^{3×4}=2^{12}$

2)定数項は0次式

$x$ が1回もかけられていない項→ $x$ が0回かけられた項→0次！

つまり、定数項(ただの数字)は、降べきの順では一番最後に書きましょう。

例) $x^2+3x+\underbrace{2}_{定数項}$

このように $x$ の降べきの順にした時は定数項は最後！

3)降べきの順（次数が高い順）に並べ、同類項ごとに計算する

例えばこんな式でみていきましょう。

例) $3x+7-2x^2+5x^2-10-7x$

$(5-2)x^2+(3-7)x+(7-10)$ 同類項にまとめる

$3x^2-4x-3$ まとめた後に計算する

　降べきの順(xの２次→１次→０次)にすると、因数分解の時にわかりやすいです

4)変数、定数の区別

例) $7xy^2$ はxについての何次式で、係数は何ですか？

答）１次式で、係数は $7y^2$ です。

まず、変数について考えていきましょう。今回の質問は $x$ について問いかけました。" $x$ について"ということは $x$ を変数、つまり全体として" $x$ についての問題"として考えるということです。

この場合は残りの $7y^2$ のことを係数と呼び、、 $y$ は7などただの数字と同じものとして考えます。この考え方は、他変数関数の最大値・最小値を求める時などに非常に大切になってきますので、ぜひ覚えておきましょう。

＊多変数関数　例） $f(x,y)=x^2+y^2-3x+5$ みたいなヤツ。

$x$ と $y$ など、複数の変数が入った式のことです。

それでは問題です。

$7xy^2$ はyについての何次式で、係数は何ですか？

答）２次式で、係数は $7x$ です。　　　もう大丈夫ですよね（笑）。

5)グループ化　 (＊正式な用語ではないですご注意を! )

式の中で部分的に、同じ数式が現れた時に、それ全体を1つの文字のように扱うことによって見通しが良くなります。それでは例をみていきましょう。

例） $(x-y+z)(2+y-x)=\{(x-y)+z \}\{2-(x-y)\}$

　　↑同じような数式 $(x-y)$ を1つの文字のように扱う

　　 $(x-y+z)(2+y-x)$

$=\{(x-y)+z \}\{2-(x-y)\}$

　　 $=-\{(x-y)+z \}\{(x-y)-2\}$ ーを外に出し、展開しましょう

$=-(x-y)^2+(2-z)(x-y)+2z$

(x-y)をカタマリとして扱いにくいと思う方は(x-y)をAなどのように他の文字で変換してみるのがオススメです。

例） $(x-y+z)(2+y-x)=\{(x-y)+z\}\{2-(x-y)\}$

　　 $x-y=A$ とすると

　　 $\{(x-y)+z\}\{2-(x-y)\}$

$=(A+z)(2-A)$

　　 $=-A^2+(2-z)A+2z$

ここまで計算したらAを $x-y$ に戻します。

置き換えで勝手に登場させた文字を残しておいてはいけません。

答) $=-(x-y)^2+(2-z)(x-y)+2z$

どうでしょうか？　もう1つ例を挙げてみます。

今度ははじめからグループ化を狙って展開していきます。

例） $x(x-1)(x-2)(x-3)$

$=\overbrace{x(x-3)}\underbrace{(x-1)(x-2)}$

$x(x-3)$ と $(x-1)(x-2)$ の組み合わせで展開します。すると

$=(\underline{x^2-3x})(\underline{x^2-3x}+2)$ 似た式が見えましたね（下線部）

$={(x^2-3x)}^2+2(x^2-3x)$ $x^2-3x$ を塊と見て展開します。

＊これもわかりにくかったら $x^2-3x=A$ など文字でおいても構いません。

　何も考えずに前から順番に展開するのではなくグループ化することによって少しでも計算を楽にすると、ミスも減っていくと思います。あと、単純に前から順番に展開すると長くなりすぎてめんどくさいですよね。

6)代入は最後に！（面倒ごとは後回し）

例） $a=x+2y,b=2x+y$ の時、 $6a^2+2b-3a(2a-1){\cdots}$ ①の値を求めよ。

このような問題で、①の式にそのまま $a=x+2y,b=2x+y$ を代入しようとする人がいますけれども、それは上記の5)で説明したグループ化をわざわざ解除してるのと同じことですので、絶対にやらないようにしましょう。

そのまま代入してしまうと結果として、式全体が長くごちゃごちゃしますので文字が消えたり、次数を間違えた、などといったミスの原因につながります。

　ではいつ代入するのかといいますと、まず①の式を計算できるところまで計算します。そして、式を簡単にしてから代入しましょう。

$6a^2+2b-3a(2a-1)=\underline{6a^2}+2b-\underline{6a^2}+3a$

下線部の同類項をまとめます。すると

$=2b+3a$

$6a^2$ と $-6a^2$ が消えて簡単な形になりました。

この簡単な形になってから最初に与えられた $a=x+2y,b=2x+y$ を代入しましょう。

この方が随分楽ですよね。

ポイントは式の形を整えてから代入することです。

7)忘れやすい公式！

ここでは皆さん忘れがちだけど重要な公式をいくつか紹介します。

1) $a^3+b^3=(a+b)(a^2-ab+b^2)$

2) $a^3-b^3=(a-b)(a^2+ab+b^2)$

3) ${(a+b+c)}^2=a^2+b^2+c^2+2ab+2bc+2ca$

4) $a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$

最低限これくらいは覚えておきましょう。思っている以上に役に立ちます。

因数分解をするときに効いてきます！

8)パスカルの三角形

最後にパスカルの三角形の話をしようと思います。

パスカルの三角形を使えば ${(a+b)}^n$ の係数が簡単に求められます。

数字の並びが ${(a+b)}^n$ の展開公式の係数と一致するのです。

パスカルの三角形の作り方は周りを全部１にしてその下の行は上の隣合う数字を足した値を書きます。

例えば２段目が1と1になっているので3段目は１と上の1と1を足した2と1の1 2 1みたいな感じです。ちょっとずれてますけど下の図を参考にしてもらえるとありがたいです。

　　　　　 1 ${(a+b)}^0$ の係数

1 1 ${(a+b)}^1$ の係数

1 2 1 ${(a+b)}^2$ の係数

1 3 3 1 ${(a+b)}^3$ の係数

1 4 6 4 1 ${(a+b)}^4$ の係数

1 5 10 10 5 1 ${(a+b)}^5$ の係数

${(a+b)}^0=1$

${(a+b)}^1=a+b$

${(a+b)}^2=a^2+2ab+b^2$

${(a+b)}^3=a^3+3a^2b+3ab^2+b^3$

${(a+b)}^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$

${(a+b)}^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5$

${(a+b)}^n$ の係数に困ったときはパスカルの三角形を書いて参考にしましょう。

　今回の記事では数学の計算が楽になったり、計算ミスをできるだけ減らすための工夫のしかたをいくつか紹介しましたので、しっかりと読み込んでもらって少しでも役立ててもらえると嬉しいです。

演算は数学の基本！侮ることなかれ！(笑)

2019-07-10

#7.5【4次元5次元…】研究者たちはなぜ高次元を考えるのか〜高校生からの質問に自分なりに答えてみた〜

深イイ話

こんにちは。医学生Gです。

#7 数の種類 part3

深イイ話

前回の記事(#6)では立方数まで紹介しましたよね。

今回はその続きとして、知る人ぞ知る少しマニアックな数を紹介していこうと思います!

1)タクシー数

　タクシー数とは２つの立方数の和としてn通りに表せる最小の正の整数のことを言います。これだけだとわかりにくいと思いますので例を見ていきましょう。

　n番目のタクシー数を $Ta(n)$ とすると

$Ta(1)=2=1^3+1^3$ １番目のタクシー数なので2つの立方数の和として1通りで表せる数のことです。

$Ta(2)=1729=1^3+12^3=9^3+10^3$ ２番目のタクシー数なので２つの立方数の和として2通りで表せる数のことです。

３番目のタクシー数ならば２つの立方数の和として3通りに、４番目ならば4通りに表すことができます。このような数のことをタクシー数といいます。

＊ちなみに３番目のタクシー数は87539319とさらにとても大きな数になります。

ここで、 $Ta(2)$ に関する有名なエピソードを紹介します。

天才数学者ラマヌジャンが診療所に入院している時に、見舞いに来たハーディさんが

「1729のナンバーのタクシーに乗ってきたが、なんの特徴もない数字だったなぁ」

という話をしたら、ラマヌジャンは

「そんなことはない。とても興味深い数字でそれは2通りの、2つの立方数の和の形で表せる最小の数です。」

とすぐさま返答したらしいです。瞬時にそんなふうに答えられるのはさすがとしか言いようがないですね。このエピソードから、1729はラマヌジャンナンバーと言われることもあります。もし身の回りでナンバーが1729の車を見つけたら、そのオーナーはこのエピソードを知っている数学オタクかも知れませんね。

2)友愛数

　友愛数とは異なる2つの自然数の組で、自分自身を除いた約数の和が互いにもう一方と等しくなるような数のことをいいます。例えば220と280の組で見ていきましょう。

220の約数は1,2,4,5,10,11,20,44,55,110,220です。

280の約数は1,2,4,71,142,280です。

　それぞれ自分自身の数字を除いた約数を足していきましょう。

220の方は1,2,4,5,10,11,20,44,55,110を全部足すと280になります。

280の方は1,2,4,71,142を全部足すと220になります。

　どうでしょう。220と280の組で自分自身を除いた約数の和が互いにもう一方と等しくなりましたね。このような数を友愛数といいます。

ロマンチック…ですかね？笑

はい、次の数にいきましょう！

3)接吻数(kissing number)

　接吻数とはn次元の単位球(中心からの距離が1の球)の周りに単位球を重ならず触れ合うように並べるとき、並べることができる最大の数のことをいいます。(次元を変えながら、1つボールに同じ大きさのボールを何個くっつけることができるかということを考えていきます。)

球と球が接していることをkissingと表現しているところがなんかオシャレですよね。そんなことは置いといて、早速例をみてみましょう。

　１次元は簡単に言えば直線のことです。直線上に単位球を並べると1つの単位球にはその両側に2つしか接することができませんよね？よって１次元の接吻数は２になります。イメージは下の図の感じです。赤色の球にいくつの球をくっつけられるかを考えていきます。

f:id:sarugorirag:20190704135435j:plain

　２次元は簡単に言えば平面のことです。1次元の単位球に対して縦方向にも単位球を追加できるようになりました。先ほどの1次元の図の上下に単位球を2つずつ加えることができますよね。よって２次元の接吻数は６になります。イメージとしてはこんな感じです。

f:id:sarugorirag:20190704135608j:plain

　３次元は２次元の平面に高さを足した空間のことです。すると２次元の図の下側(黄色い球)と上側(青い球)に3個ずつ球をさらに追加することができますよね。よって３次元の接吻数は12になります。＊下の図空間を真上から見下ろした図です。

化学で登場する六方最密構造と同じような配置になっています。

f:id:sarugorirag:20190704135616j:plain

　４次元から想像するのが難しくなってくるので飛ばしてもらっていいです。4次元を空間に時間軸を加えたもの、と考えるならば、時間軸に沿って1回移動する前後で3次元の接吻数12の状態をそれぞれ作ることができるので、接吻数は12の2倍で24となります。

5次元以上は…自分には想像できないです(泣)

今回の記事は以上になります。

マニアックな話も多かったですが、様々な数の種類があることを、面白いと思ってもらえると嬉しいです。

稀にですが、今回紹介したような教科書に載っていないことが入試問題を作るうえで題材になることもあります。雑学として知っておくと、いいことがあるかも知れませんね。

医学生Gの数学ノート

スキマ時間で読める数学の記事を数学塾講師経験のあるメンバーがお届けします！