2019-09-22

#17 三角関数公式のレシピ

高2

　「三角関数の単元、公式どんだけあるんだよ。勘弁してくれ！」

という悲嘆の叫びを最近耳にしましたので、今回はそんな方に向けた記事です。

三角関数はどうしても、アルファベットと数字が混在するイカつい感じになりがちです。そんなイメージに圧倒されて挫折しそうになるかもしれませんが一個一個丁寧に確認していけば大丈夫！自分のペースで読み進めてください。

公式を覚えるのが苦手って人は一度自分で公式を作ってみると意外と覚えられたりするものですよ。今回は#14、#15で説明した加法定理から三角関数の公式をたくさん導いていきたいと思いますので、ぜひ参考にして公式を確認してみてください。

というか、いくつも公式覚えるのは苦手！という人はこの記事を通して各公式の導出のしかたを学んでください。覚えられないのなら、自分で作ればいいのです！笑

それではゆるりとやっていきましょう！

1)加法定理

#14,15の復習です。

$\sin(α+β)=\sinα\cosβ+\cosα\sinβ\cdots①$

$\sin(α-β)=\sinα\cosβ-\cosα\sinβ\cdots②$

$\cos(α+β)=\cosα\cosβ-\sinα\sinβ\cdots③$

$\cos(α-β)=\cosα\cosβ+\sinα\sinβ\cdots④$

$\displaystyle\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}\cdots⑤$

$\displaystyle\tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}\cdots⑥$

2)２倍角の公式

２倍角の公式、こちらになります

$\sin2α=2\sinα\cosα$

$\cos2α=cos^2α-\sin^2α$

$=2\cos^2α-1$

$=1-2\sin^2α$

$\tan2α=\displaystyle\frac{2\tanα}{1-tan^2α}$

　では、この２倍角の公式がどのように作られたかわかりますか？

　なんと簡単、２倍角の公式は1)の①、③、⑤のβをαにしただけです。

$\sin(α+β)=\sinα\cosβ+\cosα\sinβ\cdots①$

$\cos(α+β)=\cosα\cosβ-\sinα\sinβ\cdots③$

$\displaystyle\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}\cdots⑤$

β＝αより

①を式変形して

$\sin(α+α)=\sinα\cosα+\cosα\sinα$

$\sin2α=2\sinα\cosα$

③を変形すると

$\cos(α+α)=\cosα\cosα-\sinα\sinα$

$\cos2α=cos^2α-\sin^2α$

　ここで、 $\underline{\sin^2α+\cos^2α=1}$ を利用すると、cosのみ、もしくはsin

のみであらわすことができますね。

cosのみで表すと $\sin^2α=1-\cos^2α$ より

$\cos2α=2\cos^2α-1$

sinのみで表すと $\cos^2α=1-\sin^2α$ より

$\cos2α=1-2\sin^2α$

⑤を変形すると

$\displaystyle\tan(α+α)=\frac{\tanα+\tanα}{1-\tanα\tanα}$

$\tan2α=\displaystyle\frac{2\tanα}{1-tan^2α}$

　こんな感じで簡単に作れましたね。加法定理さえ覚えておけば２倍角も簡単に作れちゃいます。私も忘れてしまった時は作ってた気がします（笑）。

２倍角はこれでおしまいです。まだまだ公式はたくさんありますのでどんどん見ていきましょう。

3)半角の公式

　半角の公式は先ほど求めた２倍角の公式を用いて導きます。まず、半角の公式の復習から行って見ましょう。

$\displaystyle\cos^2\frac{α}{2}=\frac{1+\cosα}{2}$

$\displaystyle\sin^2\frac{α}{2}=\frac{1-\cosα}{2}$

$\displaystyle\tan^2\frac{α}{2}=\frac{1-\cosα}{1+\cosα}$

では、ここから半角の公式にしていきましょう。

まず、2倍角の公式の $\cos2α=2\cos^2α-1$ 、 $\cos2α=1-2\sin^2α$ を変形させて、 $\cos^2α$ 、 $\sin^2α$ を求めます。

すると、

$\displaystyle\cos^2α=\frac{1+\cos2α}{2}$

$\displaystyle\sin^2α=\frac{1-\cos2α}{2}$

＊ちなみにこの2つも重要な形の一つですので覚えておきましょう。

ここまで変形できたらあとはαを $\frac{\theta}{2}$ に変えるだけです。

(αには消えてもらって、その倍の角度のθを用いた表記にチェンジします。)

$\displaystyle\cos^2\frac{\theta}{2}=\frac{1+\cos(2×\frac{\theta}{2})}{2}$

$\displaystyle\sin^2\frac{\theta}{2}=\frac{1-\cos(2×\frac{\theta}{2})}{2}$

計算して整理します

$\displaystyle\cos^2\frac{\theta}{2}=\frac{1+\cos\theta}{2}$

$\displaystyle\sin^2\frac{\theta}{2}=\frac{1-\cos\theta}{2}$

はい、おなじみのやつが出てきました！

　ちなみに $\displaystyle\tan^2\frac{\theta}{2}$ も $\displaystyle\tan^2α=\frac{\sin^2α}{\cos^2α}$ のαを $\frac{\theta}{2}$ に変えるだけです。

$\displaystyle\tan^2\frac{\theta}{2}=\frac{\sin^2\frac{\theta}{2}}{\cos^2\frac{\theta}{2}}$

$\displaystyle=\frac{\frac{1-\cos\theta}{2}}{\frac{1+\cos\theta}{2}}$

ここで分母分子を２倍すると

$\displaystyle\tan^2\frac{\theta}{2}=\frac{1-\cos\theta}{1+\cos\theta}$

これで半角の公式の導き方は終わりです。

4)3倍角の公式

ついに３倍角まできました！

　３倍角の公式は1)の①③⑤のβに2αを代入して計算するだけです。まぁ、毎回計算して導出するのはさすがに面倒ですのでこれはもう覚えてもいいと思います。

それではやっていきましょう。

$\sin(α+2α)$

$=\sinα\cos2α+\cosα\sin2α$

ここで、 $\cos2α=1-2\sin^2α$ 、 $\sin2α=2\sinα\cosα$ を代入して計算します。

$=\sinα(1-2\sin^2α)+\cosα(2\sinα\cosα)$

$=\sinα-2\sin^3α+2\sinα\cos^2α$

$=\sinα-2\sin^3α+2\sinα(1-\sin^2α)$

$=\sinα-2\sin^3α+2\sinα-2\sin^3α$

$=3\sinα-4\sin^3α$

$\underline{\sin3α=3\sinα-4\sin^3α}$

cos3αも同様に計算すると求めることができます。

$\displaystyle\underline{\cos3α=4cos^3α-3\cosα}$

5)積和、和積の公式

積和と和積は結構微分積分の分野で使う機会が多いような気がしますので、しっかりマスターしたいところです。

これは加法定理を足したり引いたりして2で割るだけで作れますので試験中に忘れてしまっても簡単に作れちゃいます。

①＋②より

$\sinα\cosβ=\frac{1}{2}\{\sin(α+β)+\sin(α-β)\}$

①ー②より

$\cosα\sinβ=\frac{1}{2}\{\sin(α+β)-\sin(α-β)\}$

③＋④より

$\cosα\cosβ=\frac{1}{2}\{\cos(α+β)+\cos(α-β)\}$

③ー④より

$\sinα\sinβ=-\frac{1}{2}\{\cos(α+β)-\cos(α-β)\}$

※最後のsinαsinβはマイナスを付け忘れないようにしましょう！

これで積和は終わりです。次に和積も出していきます。

　ここで、α+β=A、α-β=Bとすると、

$α=\frac{A+B}{2}$ 、 $β=\frac{A-B}{2}$ となります。

(α+β=Aとα-β=Bの両辺を足したり引いたりしてみてください。)

これを上の積和の公式に代入して両辺を２倍すると完成します。

$\displaystyle\sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$

$\displaystyle\sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2}$

$\displaystyle\cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}$

$\displaystyle\cos A-\cos B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2}$

※最後のcosA-cosBはマイナスを付け忘れないようにしましょう！

これで積和もおしまいになります。

　今回は三角関数の公式についてまとめて見ました。半角の公式や積和の公式は三角関数の次数を下げることができますので、三角関数がからむ積分で大活躍します。今回の記事の内容をマスターしていれば、角度がからむ図形の問題や数Ⅲの複素数平面、積分、時には物理の波の問題など、様々な場面で三角関数を用いて解けるようになります。ぜひぜひ、読み込んで、自力で導出できるようにトレーニングしてくださいね。

2019-09-18

#16 合成公式はsinだけじゃないんです！

高2

お久しぶりです。医学生Gです。

今日は多忙のためちょっとテンション高めでお送りします。簡単な内容の記事を書くつもりが、思いついたことをあれこれ書いていると意外にハイレベルな記事となってしまいました。無理だと思ったら適宜飛ばしながら読んでください。それでは本日の講義、スタートです！

数II 三角関数の単元では合成公式を学習すると思います。

sinとcosの和がsinのみの式に変幻するやつです。覚えていますか？

教科書ではこのsin合成がメインになっていると思いますが実はcos合成というものもあるんです。今回は普段は登場しないcos合成の話も含めて、合成公式のいろいろな魅力をご紹介します。

1) まずはsin合成の復習から。

$a\sin{\theta}+b\cos{\theta}=\sqrt{a^2+b^2}\sin(\theta+\alpha)$

というやつですね。これを導出しておきます。

ポイントは3つです。

・ $\sqrt{a^2+b^2}$ を無理やりくくり出すこと

・三角形をイメージして新たな角度を登場させること

・加法定理を逆向きに使うこと

それではいってみましょう！

$a\sin\theta+b\cos\theta$

$\displaystyle=\sqrt{a^2+b^2}(\frac{a}{\sqrt{a^2+b^2}}\sin\theta+\frac{b}{\sqrt{a^2+b^2}}\cos\theta)$ ←無理やりくくり出す

$=\sqrt{a^2+b^2}(\cos\alpha\sin\theta+\sin\alpha\cos\theta)$ ←αが登場

$=\sqrt{a^2+b^2}\sin(\theta+\alpha)$ ←加法定理

αが登場する部分は次のような直角三角形を考えています

f:id:sarugorirag:20190917093152j:plain

a,bの値に合わせて適切な角度αを自分で新たに登場させたわけです。

問題の解答を書くときには、勝手に登場させた角度αについて、

“但しαは $\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}$ を満たす鋭角”

などというように紹介をしておくことがマナーです。

(注)いつも鋭角になるとは限りません！

それでは前置きはこれくらいにして、cos合成の話を始めます！

cos合成の式は $\displaystyle{c\cos\theta+d\sin\theta=\sqrt{c^2+d^2}\cos(\theta-\beta)}$ です。

2) cos合成の導出その1

まずは基本的な導出からやってみようと思います。

先ほどのsin合成と同様の手順で導きますので、どこが同じでどこが異なるかをチェックしながらみてくださいね。

$c\cos\theta+d\sin\theta$ ←cos sin の順番に並べた方がわかりやすいと思います

$\displaystyle=\sqrt{c^2+d^2}(\frac{c}{\sqrt{c^2+d^2}}\cos\theta+\frac{d}{\sqrt{c^2+d^2}}\sin\theta)$ ←無理やりくくり出す

$=\sqrt{c^2+d^2}(\cos\beta\cos\theta+\sin\beta\sin\theta)$ ←βが登場

$=\sqrt{c^2+d^2}\cos(\theta-\beta)$ ←加法定理

今回βを登場させるにあたって考えた直角三角形は次のようなものです。

f:id:sarugorirag:20190917093217j:plain

3) cos合成の導出その2

先ほどとは異なるcos合成の導出の方法として、ベクトルを用いたものをご紹介します。ベクトルをまだ習っていない方には少し難しいかもしれませんが、ベクトルを習得している人にとっては美しすぎて感動するレベルですのでお付き合いください。

少しだけベクトルの復習をしておきましょう。

2つのベクトル $\vec{a}=(x_a,y_a)$ と $\vec{b}=(x_b,y_b)$ について

これらのなす角を $\theta$ とすると

内積は $\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

と定義されますがベクトルの成分を用いて

$\vec{a}\cdot\vec{b}=x_ax_b+y_ay_b$ とも計算できます。

つまりベクトルの内積の計算方法は２つあるということです。

それではこれを踏まえてcos合成の導出をしてみましょう。

おもむろに２つのベクトルを

$\vec{p}=(c,d)$ , $\vec{e}=(\cos\theta,\sin\theta)$ とおき、

それぞれがx軸となす角を $\beta , \theta$ とします。

するとこれら２つのベクトルのなす角は $(\beta-\theta)$ となりますね。

f:id:sarugorirag:20190918090905j:plain

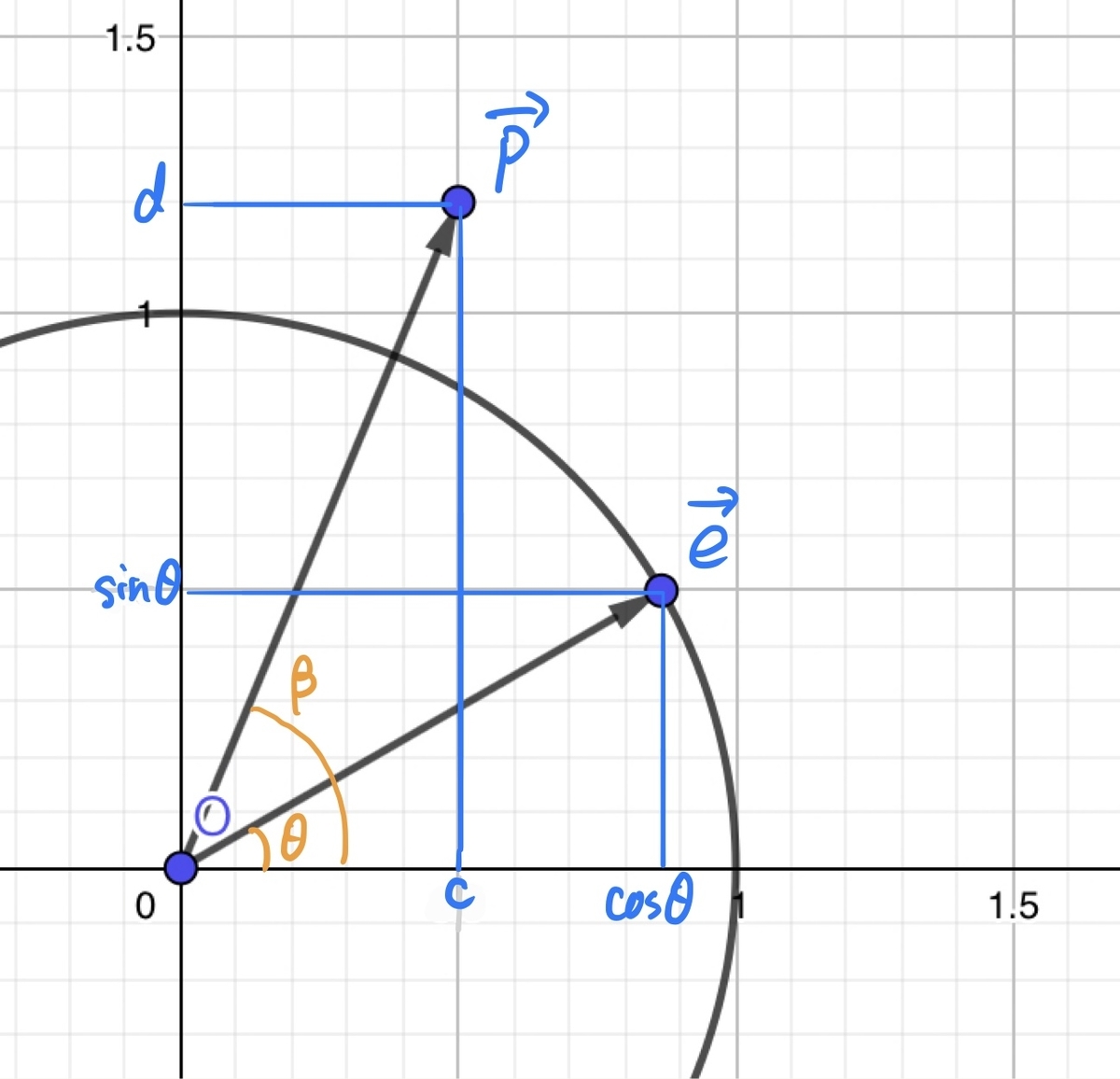
それでは内積を計算します。

定義で計算すると

$\vec{p}\cdot\vec{e}=|\vec{p}||\vec{e}|\cos(\beta-\theta)$

$=\sqrt{c^2+b^2}\sqrt{cos^2\theta+sin^2\theta}\cos(\beta-\theta)$

$=\sqrt{c^2+b^2}\cos(\beta-\theta)$

$=\sqrt{c^2+b^2}\cos(\theta-\beta)\cdots①$ (∵ $\cos(-\theta)=\cos\theta$ )

成分で計算すると

$\vec{p}\cdot\vec{e}=c\cos\theta+d\sin\theta\cdots②$

$①=②$ より、

$c\cos\theta+d\sin\theta=\sqrt{c^2+d^2}\cos(\theta-\beta)$

となります。

やってることは内積の計算だけ！シビれますよねぇ。

美しい導出だと思いませんか？笑

他に幾何的な導出の方法などもありますので興味がある人は調べてみてくださいね。

4) cos合成を知っておくメリット

cos合成を知っておくと、sinにまとめるかcosにまとめるかを自由に選択することができます。

例えば最大最小をもとめる場合を考えると、単位円においてsinの場合大小を上下(y軸)方向で考えますが、cosでは左右(x軸)方向で考えます。このようにsinとcosにはそれぞれ性格が異なる部分がありますので、状況に応じて使い分けることができると武器になりますね。

そして最大のメリットは数Ⅲで登場する極方程式と相性が抜群に良いことではないでしょうか。

円、放物線、楕円、双曲線など焦点を持つ曲線は通常cosを含む極方程式で表されます。(離心率eが頭に浮かんだ人はバッチリですね。)

直線の式もcosを含む極方程式で表すことができます。

よって高校範囲で登場する極方程式に三角関数が含まれているならば、十中八九それはcosなんですよね。（ ※ sinで表せないこともないですが、式が汚くなることが多いです。）

だったら、最初からcosにまとめた方が楽じゃないですか？

例として、x,yを用いて表されている直線の方程式をr,θを用いる極方程式に変換する場合を考えてみましょう。

$x+\sqrt{3}y=2$

⇨ $r\cos\theta+\sqrt{3}r\sin\theta=2$

$r(\cos\theta+\sqrt{3}\sin\theta)=2$

$r(2\cos(\theta-\frac{\pi}{3}))=2$

$r\cos(\theta-\frac{\pi}{3})=1$

という感じです。合成のみで式が整いましたよね。

数Ⅲを学習される方はcos合成ができると便利だと思います。

5) 合成の本質

合成公式を使ったsinとcosの合成は、“波の合成”に他なりません。このことを説明しておきます。

例として sin(x)+cos(x) をsin合成すると $\sqrt{2}\sin(x+\frac{\pi}{4})$ となるのですが、これらのグラフを見てみましょう。

f:id:sarugorirag:20190918195403j:plain

青がy=sin(x) ,緑がy=cos(x) ,オレンジが $y=\sqrt{2}\sin(x+\frac{\pi}{4})$ のグラフです。

縦に見てみると、オレンジが青と緑の高さの合計を表していませんか？

このように、合成公式というのは波の足し算を式で表しているだけのものなのです。

ちなみにこの“波の合成”は物理現象として海面上などで実際に起きています。自然現象の謎を解き明かす為に数学が有効となる良い例ですね。

あと、cos合成したらどうなるの？という疑問にお答えしておきます。

sin(x)+cos(x)をcos合成すると $\sqrt{2}\cos(x-\frac{\pi}{4})$ となりsin合成とは一見違った式が出てきますが、 $\sin(\frac{\pi}{2}-\theta)=\cos\theta$ と $\cos(-\theta)=\cos\theta$ を使って変形すると

$\sqrt{2}\sin(x+\frac{\pi}{4})$ ←sin合成

$=\sqrt{2}\sin(\frac{\pi}{2}-(-x+\frac{\pi}{4}))$

$=\sqrt{2}\cos(-x+\frac{\pi}{4})$

$=\sqrt{2}\cos(x-\frac{\pi}{4})$ ←cos合成

となるので、sin合成で得られた式とcos合成で得られた式は見た目は違えど同じ波を表す同一のものであることがわかります。同じ結果になるからこそ、sin合成とcos合成、好きな方を使って良いということになるのですね。

今回の内容は以上になります。cos合成は知る人ぞ知る有名な裏技ですので知っておいて損はないでしょう。実際にcos合成で瞬殺できる問題がセンター試験で過去に出題されています。

ここまで読んでチンプンカンプンだっだ人は今はわからなくてもいいですが、要するに三角関数はいろいろな性質を併せ持ち、数学や物理などのさまざまな分野と関連している非常にExcitingなものだということです。三角関数を極めれば数式の見え方が変わってくると思いますので重点的に勉強してくださいね。それでは。おやすみなさい。

2019-09-07

#15.5【2020年度大学入試予想問題】

深イイ話

おひさしぶりです。

2020年度入試にどこかの大学で出題されそうな問題を思いつきましたので共有しておきたいと思います。

早速ですが問題はこちらです！

f:id:sarugorirag:20190906225344j:plain

数Aの整数の単元を履修していれば解けると思います。

基本の確認ができる良問ではないかと自負しておりますので、皆さん是非考えてみてくださいね(^^)

ハイレベルな方、物足りなかったらゴメンナサイ💦

考えた人は以下の解答を見てみてください。

わからない人は回答の前にヒントを乗せておきますので参考にしてください。

[ヒント]

条件Bについて

6,7,8,9で割って4余る数を考える前に、とりあえず6と7で考えてみよう。

6で割って４余る数	4	10	16	22	28	34	40	46	52
7で割って４余る数	4	11	18	25	32	39	46	53	60

上の表のように6で割って４余る数と7で割って４余る数を並べて見ました。では、6で割っても7で割っても４余る数はどこでしょうか。赤文字になってる4と46です。46の次の数は何になるでしょうか。6と7の最小公倍数である42ごとに間隔を空けて存在すると思いませんか。実際に4と46も42の間隔が空いてます。

　つまり、6と7両方で割っても４余る数は　42n+4 (nは整数) の形で表すことができると考えられます。それでは、6,7,8,9で割って4余る数は…???

それでは後は解答を参考にしてください。

[解答]

まず条件Bについて考える。

6,7,8,9の最小公倍数は504 ( $2^3×3^2×7=504$ )であるということから、“6,7,8,9のいずれの数で割っても4余る自然数” は、504ごとに間隔を空けて存在する。さらに4 は “6,7,8,9のいずれの数で割っても4余る自然数” であることから

xは整数nを用いて

$x=4+504n\cdots①$

と表すことができる数といえる。

さらに条件Aより、

xは整数mを用いて

$x=101m\cdots②$

とも表すことができる。

①、②より

$4+504n=101m$

即ち、

$101m-504n=4\cdots③$

となる整数m,nが存在すれば良い。

ユークリッドの互除法より

$504=101*4+100$

$101=100*1+1$

であるので、

$101=(504-101*4)*1+1$

よって

$101*5-504*1=1$ (←これがすぐ思いつく人は互除法しなくていいです。)

両辺4倍して、

$101*20-504*4=4\cdots④$

③ー④より

$101(m-20)-504(n-4)=0$

よって

$101(m-20)=504(n-4)\cdots⑤$

ここで、101と504は互いに素であるから、（※101は素数だよ）

⑤より、整数kを用いて

$\begin{cases}m-20=504k\\n-4=101k\end{cases}\$

即ち

$\begin{cases}m=504k+20\\n=101k+4\end{cases}\$

となる。

この結果を②に代入すると

$x=101×(504k+20)$

$=50904k+2020$ (kは整数)

このように表される数であれば条件A,Bを満たす。

最後に条件Cよりxは50000以下の自然数であるから、

kは $0＜50904k+2020≦50000$ を満たす整数でなければならない。

すると、この条件を満たすのは k=0 の場合のみに限られるので

求める自然数xは $50904*0+2020=\underline{2020}$ のみである。

っという感じの問題でした！

答えが2020になる問題…どっかの私立大学で出題されないですかね？笑

　後半に登場する、ユークリッドの互除法を含めた不定方程式の解き方は重要なのでしっかり復習しておいてください。

ここで受験生の皆さんにお送りする大事なポイント！

2020という数には以下のような特徴があります。

① 素因数分解すると　 $\underline{2^2*5*101}$

② 6,7,8,9のいずれの数で割っても4余る

③ 2通りの平方和で表すことができる　 $\underline{16^2+42^2=24^2+38^2=2020}$

今回は①と②の性質を使って問題を作りました。

今回は登場しなかった③の特徴も結構凄いですよね。

知っておくといいことがあるかもしれません。

この記事を読んでくださる皆さんが1点でも多く得点できますように！

と、ただただお祈りする医学生Gでした。

ガンバレ受験生！(^^)

2019-08-25

＃15 加法定理その２　遊んで加法定理を理解しよう！

高2

　前回、加法定理を単位円で証明しましたけれども、ちゃんと理解できましたか？

今回は加法定理を長方形を使って証明しようと思います。

角度が限定されてしまうため、完璧な証明とは言えないのですが、遊びだと思って付き合ってください。

　後半は#13でやった90°+θを加法定理を使って実際に出してみようと思いますので、最後まで読んでみてください。

1)長方形を使ったお遊び！

　加法定理、長方形を使って証明する方法を知ってましたか。結構面白いですのでみていきましょう。

f:id:sarugorirag:20190823164836p:plain

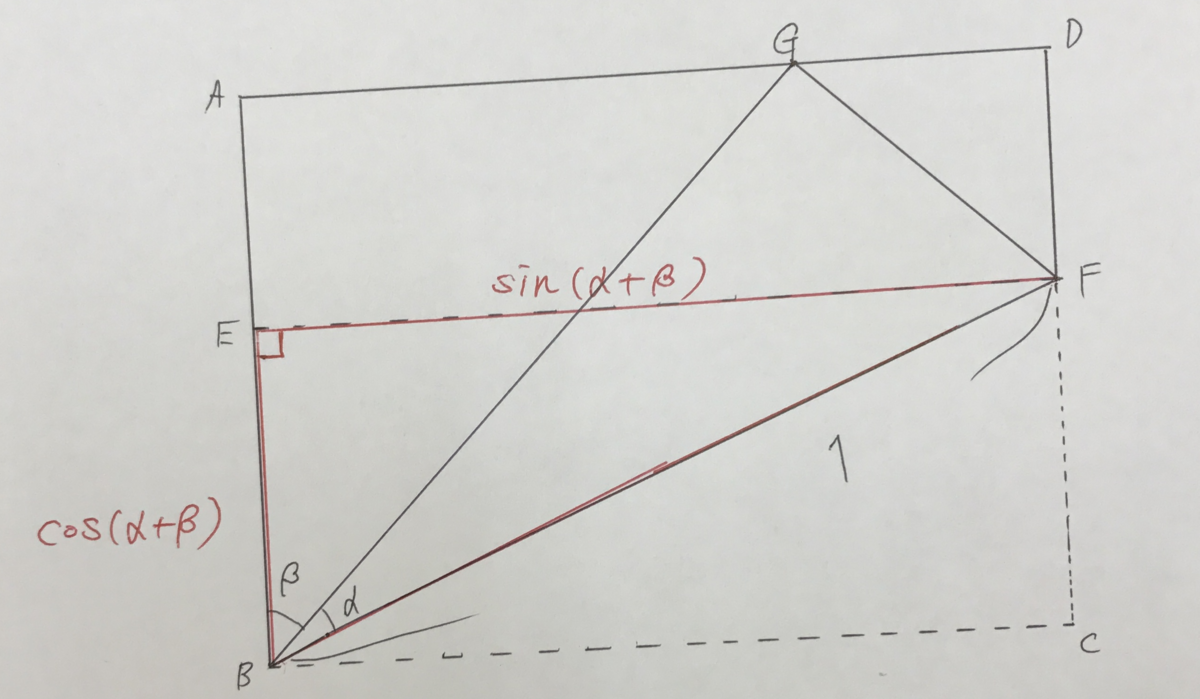
　ちょっと斜めになってしまって申し訳ないんですが、上図のように点Cを点Gのところまで長方形を折り曲げます。そしてBF=1、 $\angle{GBF}=α$ 、 $\angle{GBA}=β$ と設定します。

　こうすると $\angle{FBA}=α+β$ になります。ここで上図の赤い三角形である△FBEに注目してください。BF=1ですので、sin、cosを取るとEF=sin(α+β)、EB=cos(α+β)になりますね。

　とりあえず、sin(α+β)がEFの長さ、cos(α+β)がEBの長さなのを覚えておいてください。以下はこのEF、EBの長さをα、βを用いて求めていきます。

f:id:sarugorirag:20190823165823p:plain

　次に、注目する三角形を変えましょう。上の図の青い三角形である△GBFに注目しましょう。

$\angle{GBF}=α$ でBF＝１ですので、△GBFで同じようにsin、cosを取るとGF=sinα、GB=cosαになります。

f:id:sarugorirag:20190823170618p:plain

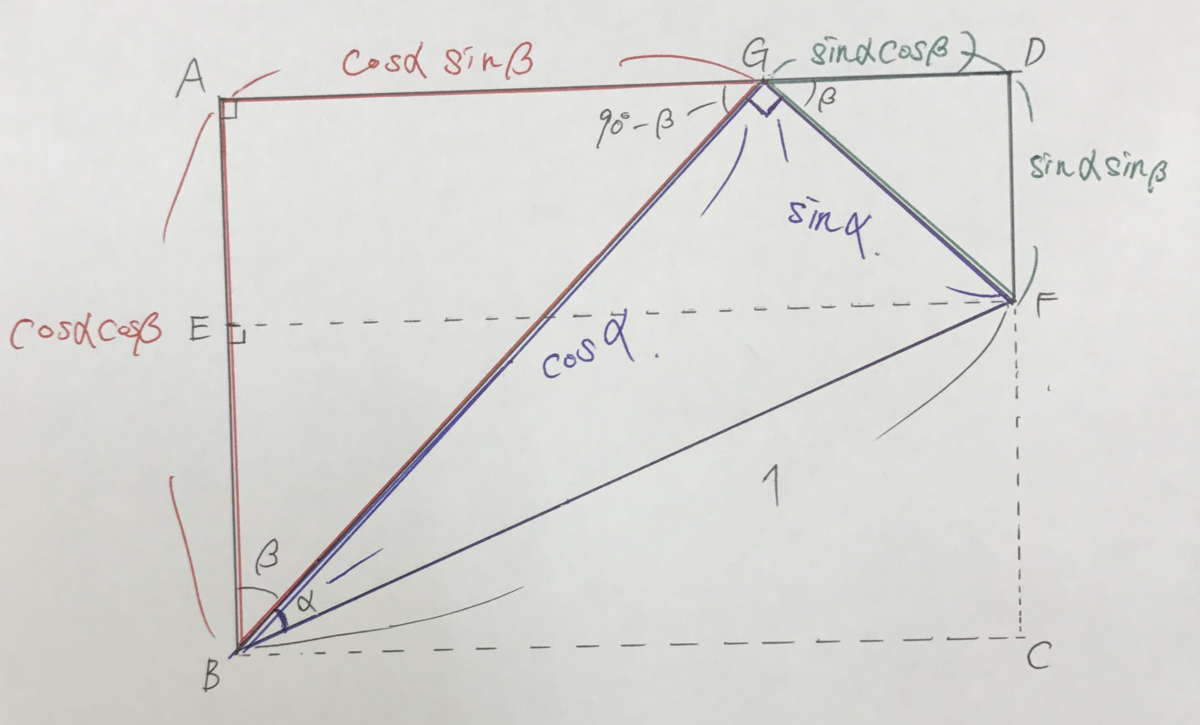
　GF=sinα、GB=cosαを前の画像のところで求めました。

そしたら、まずはGF=sinαを含む三角形から見ていきましょう。

　GFを含む三角形は△GFDで上の図の右上の緑色の三角形です。

上図のように $\angle{AGB}=90°-β$ 、 $\angle{BGF}=90°$ ですので、

$90°-β+90°+\angle{FGD}=180°$

$\angle{FGD}=β$ になります。

そうするとGF=sinαだから残りの辺の長さGD=sinαcosβ、DF=sinαsinβになりますね。

この２辺は最初のEF、EBを求めるのに必要です。

f:id:sarugorirag:20190823172543p:plain

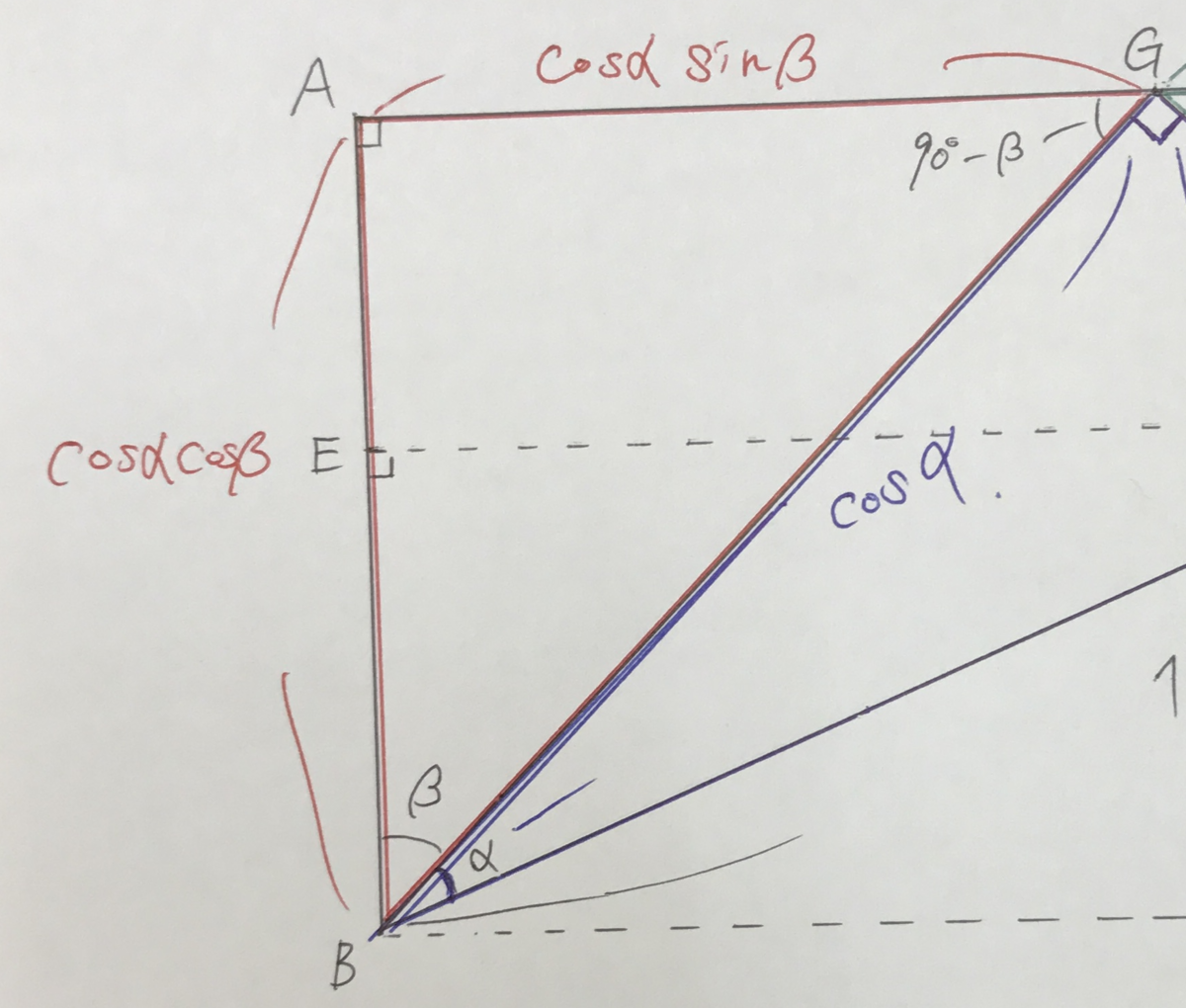
次に、GB=cosαを含む三角形である△GBAについて見てみよう。

GB=cosα、 $\angle{GBA}=β$ ですので、これも残りの辺の長さを求めていきましょう。これも、sin、cosを取るとAG=cosαsinβ、AB=cosαcosβになりますね。

この２辺もEF、EBの辺を求めるのに必要です。

ここまでの話は理解できましたか？そしたら今まで求めてきた辺を使ってsin(α+β)、cos(α+β)であるEF、EBを求めていきましょう。

f:id:sarugorirag:20190823170618p:plain

上の図を参考にして見ていきましょう。

EFの長さは長方形の上辺であるAGとGDを足した長さですね。また、EBの長さはABからAE(=DF)を引いた長さに一致しますね。これを実際に長さを代入して求めていきます。

すると、

EF=sin(α+β)=AG+GD=cosαsinβ+sinαcosβ

EB=cos(α+β)=AB-DF=cosαcosβ-sinαsinβ

　出てきましたね、sin(α+β)、cos(α+β)が。こんな感じで長方形を用いて加法定理を導出することができます。

　最初にも言いましたが、この求め方は角度が限定されているため、証明には使えませんが、雑学として覚えておくといいかなと思います。

2)加法定理を使って90°+θのやつを求める

　#13でやった90°+θのやつを実際に加法定理を用いてsin(90°+θ)、cos(90°+θ)を求めてみましょう。

sin(α+β)=cosαsinβ+sinαcosβ

cos(α+β)=cosαcosβ-sinαsinβ

実際にα=90°、β=θを代入してやってみましょう。

sin(90°+θ)

=cos90°sinθ+sin90°cosθ

=cosθ

＊cos90°=0、sin90°=1

cos(90°+θ)

=cos90°cosθ-sin90°sinθ

=-sinθ

　図を描くのが苦手な人は加法定理を使って求めるのもいいと思います。sin、cosのどちらかが0になりますので、簡単に求めることができます。ちなみに私は加法定理で頭の中でやってました（笑）。

　今回は長方形を使った加法定理の証明と実際に加法定理を使ってsin(90°+θ)、cos(90°+θ)を求めてみました。長方形の方はお遊びですので、加法定理の証明問題がでてきたら書かないように気をつけましょう。まぁ、もし単位円が思いつかなかったら書いてみるのもアリだとは思いますが（笑）。90°+θのやつは図を書いてもよし、加法定理で求めてもよしですので、自分に合う方法でやるのがいいと思います。今回の記事を読んで数学をより深く理解してもらえると嬉しいです。

いろんな考え方を知っておくということが難関大数学に立ち向かう上で強みになると思いますよ。(^^)

2019-08-21

#14 加法定理登場！その１

高2

　おはようございますこんばんは、医学生Gです。みなさん、加法定理はもう学校で習いましたか？長い式を丸暗記しなくてはならない…と思うと辛くなりますよね。今回は加法定理を単位円を使って証明する方法を紹介していきたいと思いますので、1)~2)まで読んでみてください。

1)加法定理

　まず、加法定理の確認から。

$\sin(α+β)=\sinα\cosβ+\cosα\sinβ$

$\sin(α-β)=\sinα\cosβ-\cosα\sinβ$

$\cos(α+β)=\cosα\cosβ-\sinα\sinβ$

$\cos(α-β)=\cosα\cosβ+\sinα\sinβ$

式の真ん中の符号はプラマイマイプラで覚えよう！

$\displaystyle\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}$

覚え方は”イチマイタンタンタンプラタン”←グラタンみたいで美味しそうですね（笑）

$\displaystyle\tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}$

ちなみに、tan(α+β)、tan(α-β)の式の真ん中の符号も上からプラマイマイプラになっていますね。

2)単位円での証明

これは実際に東大の入試問題として出題されたこともあります。基本をしっかり押さえよという東大からのメッセージですね。(1)〜(5)まであります。

(1)cos(α+β)

f:id:sarugorirag:20190819210020p:plain

上図のように点と角度を設定します。

A(1,0)、B( $\cosα$ , $\sinα$ )、C( $\cos(α+β)$ , $\sin(α+β)$ )、

D( $\cos(-β)$ , $\sin(-β)$ )=( $\cosβ$ , $-\sinβ$ )、＊β１＝β

f:id:sarugorirag:20190819211908p:plain

　上図のように、補助線を引くと三角形が2つできますね。
　ここで、△AOCと△BODは、２辺とその間の角が等しいため△AOC≡△BODであると言えます。

CA=BDなので各点の座標を用いて以下のように立式すると、

$(CA)^2=(BD)^2$ より

$\{1-\cos(α+β)\}^2+\sin^2(α+β)=(\cosα-\cosβ)^2+(\sinα+\sinβ)^2$

展開すると、

$1-2\cos(α+β)+\cos^2(α+β)+\sin^2(α+β)$

$=\cos^2α-2\cosα\cosβ+\cos^2β+\sin^2α+2\sinα\sinβ+\sin^2β$

$\sin^2+\cos^2=1$ より

$1-2\cos(α+β)+1=1+1-2\cosα\cosβ+2\sinα\sinβ$

式を整理します。

$-2\cos(α+β)=-2\cosα\cosβ+2\sinα\sinβ$

全体を-2で割りると

$\underline{\cos(α+β)=\cosα\cosβ-\sinα\sinβ}$

これで $\cos(α+β)$ の証明が終わりました。

以下の(2)〜(4)はcos(α+β)をベースに考えますので、最低でも(1)はしっかりと覚えておきましょう。

(2)cos(α-β)

$\cos(α-β)$ の証明はβを-βに変えるだけです。

$\cos(α-β)$

$=\cosα\cos(-β)-\sinα\sin(-β)$

$=\cosα\cosβ+\sinα\sinβ$

$\underline{\cos(α-β)=\cosα\cosβ+\sinα\sinβ}$

(3)sin(α+β)

ここから $\sin(α+β)$ の証明をしたいと思います。

　以前の記事#13で説明した90°+θのθを-θに変えただけである90°-θを利用すると、cosをsinに変えることができます。　　　　　

＊cos(90°-θ)＝sinθ

これを利用すると

$\sin(α+β)$

$=\cos \{90°-(α+β)\}$

ここで90°-(α+β)を(90°-α)と-βに分けます

$=\cos \{(90°-α)-β)\}$

$=\cos(90°-α)\cosβ+\sin(90°-α)\sinβ$

$=\sinα\cosβ+\cosα\sinβ$

$\underline{\sin(α+β)=\sinα\cosβ+\cosα\sinβ}$

これで $\sin(α+β)$ の証明は終わりです。

(4) sin(α-β)

$\sin(α-β)$ は $\cos(α-β)$ の時と同じでβを-βに変えます。

すると、

$\sin(α-β)$

$=\sinα\cos(-β)+\cosα\sin(-β)$

$=\sinα\cosβ-\cosα\sinβ$

$\underline{\sin(α-β)=\sinα\cosβ-\cosα\sinβ}$

(5)tan(α+β)、tan(α-β)

tan(α+β)、 tan(α-β)は $\underline {\tanθ= \frac{ \sinθ}{ \cosθ}}$ を利用して求めます。

$\tan(α+β)$

$= \displaystyle\frac{ \sin(α+β)}{ \cos(α+β)}$

$=\displaystyle\frac{\sinα\cosβ+\cosα\sinβ}{\cosα\cosβ-\sinα\sinβ}$

ここで、分母分子をcosαcosβで割ります。

すると、

$=\displaystyle\frac{ \frac{\sinα}{\cosα}+\frac{\sinβ}{\cosβ}}{1-\frac{\sinα\sinβ}{\cosα\cosβ}}$

$\tanθ= \frac{ \sinθ}{ \cosθ}$ を利用して整理すると、

$\underline{\displaystyle\tan(α+β)=\frac{\tanα+\tanβ}{1-\tanα\tanβ}}$

$\tan(α-β)$

$= \displaystyle\frac{ \sin(α-β)}{ \cos(α-β)}$

$=\displaystyle\frac{\sinα\cosβ-\cosα\sinβ}{\cosα\cosβ+\sinα\sinβ}$

これも分母分子をcosαcosβで割ります。

すると、

$=\displaystyle\frac{\frac{\sinα}{\cosα}-\frac{\sinβ}{\cosβ}}{1+\frac{\sinα\sinβ}{\cosα\cosβ}}$

また $\tanθ= \frac{ \sinθ}{ \cosθ}$ を利用して整理しましょう！

$\underline{\displaystyle\tan(α-β)=\frac{\tanα-\tanβ}{1+\tanα\tanβ}}$

　長々となりましたが、これで全ての加法定理の証明が終わりましたね。

　加法定理の証明はまず単位円を用いてベースである $\cos(α+β)$ を求めてから、残り3つをこんな感じで証明しますので、一度はしっかりと理解してください。最低でも(1)はできるようにしましょう。東大が以前出しているので、もしかしたらあなたが受ける大学の入試問題で出るかもですよ?（笑）

　次回の記事は長方形を使った、直感的に分かりやすい加法定理の説明をしますので、ぜひそちらも読んでみてください。今回の記事で加法定理の証明はしっかりと覚えておきましょう。

2019-08-15

#13.5 tanのグラフはなぜ途切れるのか

深イイ話

最近、とある勉強熱心な方から

「tanのグラフはなぜ途切れるのか。

tan90°についてどのように理解しておけば良いのか。」

という質問をいただきましたのでその回答をこの場で共有しておこうと思います。

1)三角関数の定義

まず大前提として今回の回答にあたっては、三角関数の定義は単位円を用いたものとします。

直角三角形を用いた定義では0<θ<90°の範囲に限られているのでθが90°になる瞬間について考えることができませんからね。

以下、記事#11の復習になりますが

f:id:sarugorirag:20190727115056p:plain

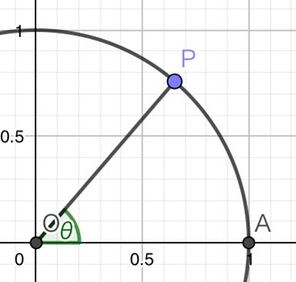
上の図において(1,0)を点A、単位円周上の点を点Pとし、 $\angle{AOP}=\theta$ と定めた時の点Pの座標を(sinθ,cosθ)とします。sin,cosを点Ｐの座標として定義することにより0<θ<90°の制限がなくなり、回し放題になるのでした。覚えていますか？

ここで、 $tan\theta=\frac{sin\theta}{cos\theta}$ ですが、直線OPの傾きも同じく $\frac{sin\theta}{cos\theta}$ の値をとりますので、tanθは直線OPの傾きといえます。

2)傾きの定義から考える

さて、 1) で「tanθは傾き」と述べましたが傾きの定義は覚えていますか？

中学で学ぶ内容ですが

$(傾き)=\frac{(yの増加量)}{(xの増加量)}$ というやつです。

一次函数 $y=ax+b$ のaの部分が、傾きの値になっているんでしたよね。

例えば次の図のような場合には

f:id:sarugorirag:20190814224826j:plain

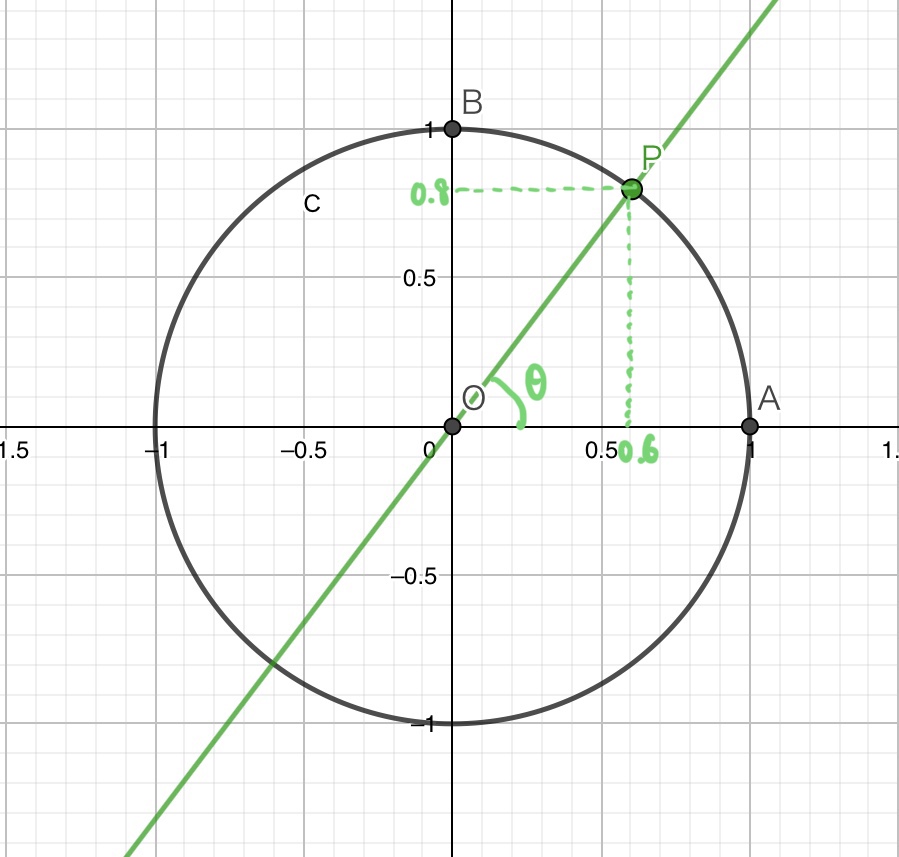
傾きは $\frac{(yの増加量)}{(xの増加量)}\quad=\frac{0.8}{0.6}=\frac{4}{3}$ となります。

このように、”xの増加量”と”yの増加量”のふたつの値から傾きを計算できるわけですが、θが90°となる場合はどうでしょうか。次の図のような状態になっていますね。

f:id:sarugorirag:20190814230408j:plain

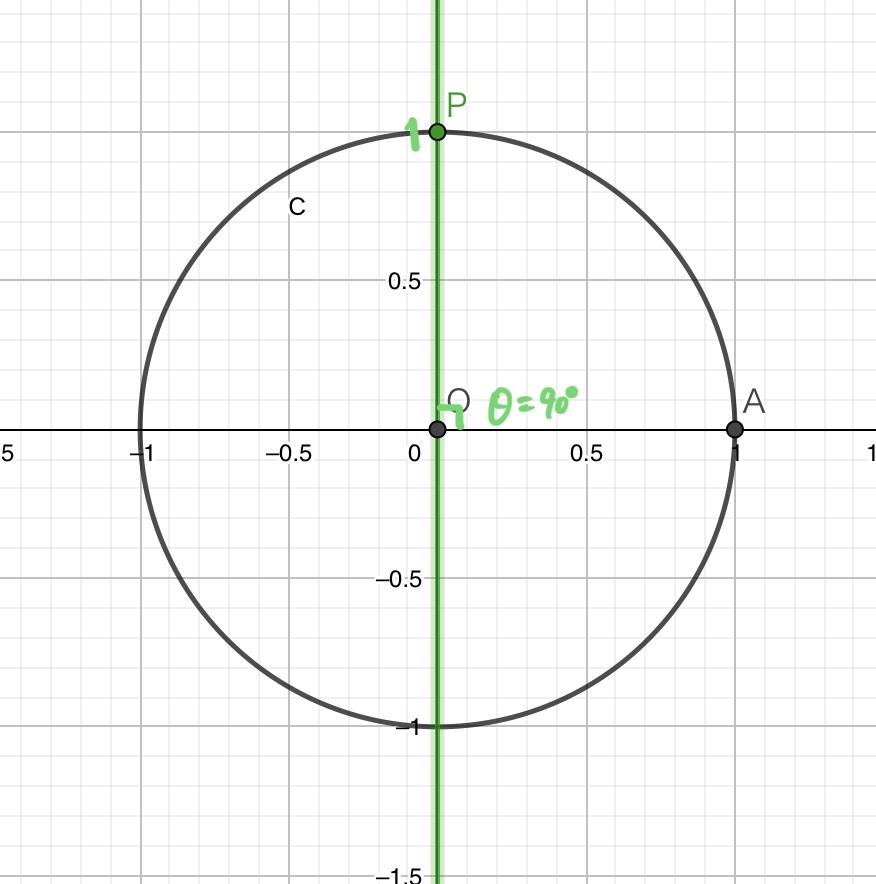
気づきましたか？困りますよね。

$(傾き)=\frac{(yの増加量)}{(xの増加量)}$ を計算しようとしても、xの増加量というやつがないんです。分母に入れる数字がない！困った！！

2点P,Oの間にx座標の差が少しでもあれば計算できるのですが、今回のように直線OPが完全な縦線になる場合にのみ、傾きは計算不能となります。

よってこのようなy軸と平行な直線(縦線)に対して、傾きは定義できないのです。「こーゆー縦線のとき、傾きは計算しないの！ (怒)」という約束になっているのですね。

ここまでのまとめ

θ=90°のとき、傾きは無し(定義外)。そのためtanθの値もなし。

値なしの部分があるため、tanのグラフは途切れるのです。(下図)

f:id:sarugorirag:20190814232459j:plain

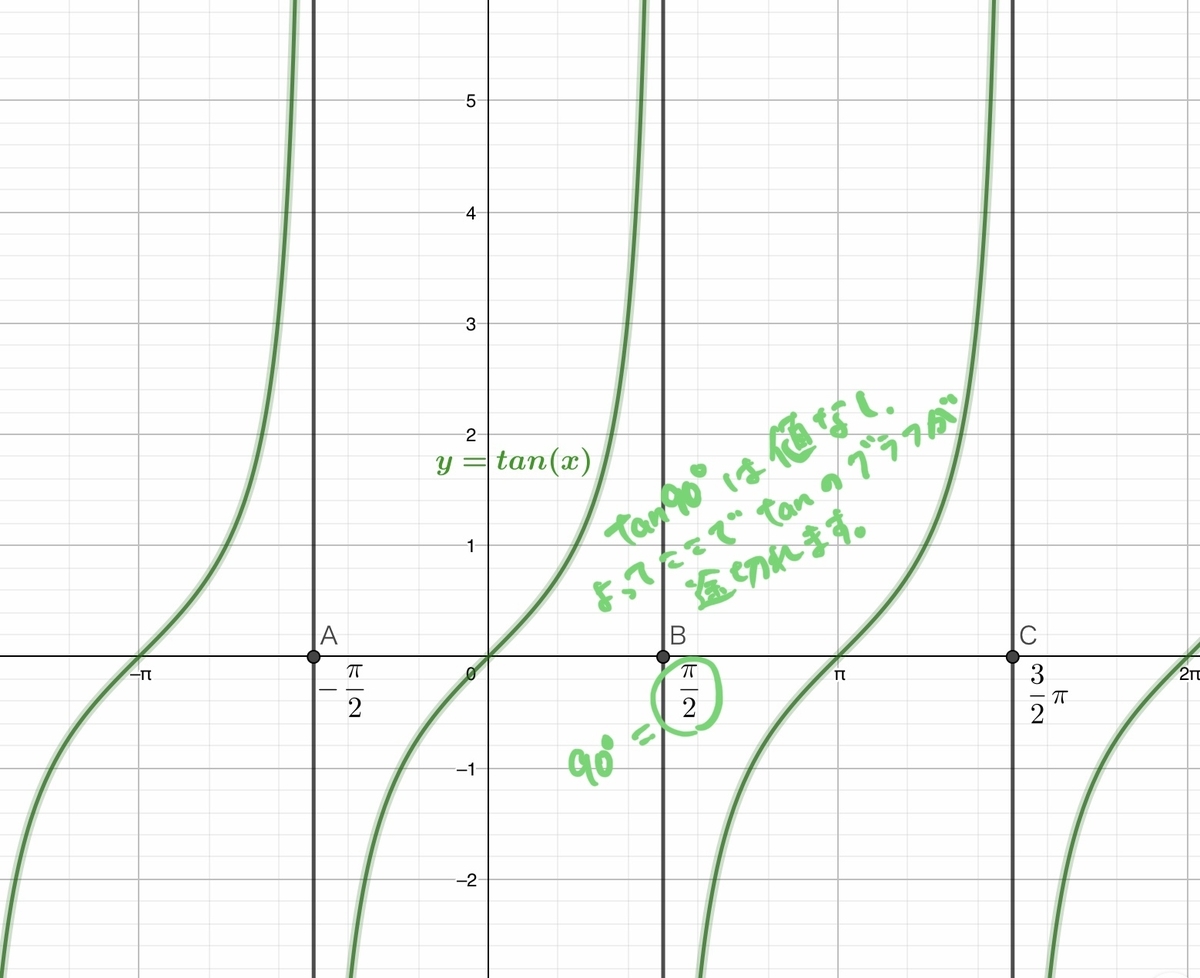
この説明で納得していただけたでしょうか？

納得できた方はここまでで終わってもらってオッケーです。

でも勘のいい人なら「xの増加量を0にして傾きの計算を強行すれば良い」と考えることでしょう。そんな方への説明をこれからしていきます。

少し踏み込んで、「極限」の考え方が登場します。準備はいいですか？

3)極限を用いた考え方

xの増加量を0として、計算を強行してみましょう。

O(0,0) P(0,1) ですので

$\frac{(yの増加量)}{(xの増加量)}\quad=\frac{1}{0}$

分母が0の分数が出てきました。なんだコイツはって感じですよね。

それもそのはず。こんな数字はないんです。0をいくつ合わせても1にはなりませんからね。そこで、極限という考え方で、それっぽい答えを探しにいきます。

$\frac{1}{1}$ をスタートにして分母をどんどん小さくしていき、0に近づけていきます。

$\frac{1}{1}=1$

$\frac{1}{0.1}=\frac{10}{1}=10$

$\frac{1}{0.01}=\frac{100}{1}=100$

$\frac{1}{0.001}=\frac{1000}{1}=1000$

分母が0に近づくほど数が大きくなっていくのがわかりますか？

このノリで、「分母が0になるときには限りなく大きい数になるのだろう」

と考え、「 ∞:無限大」という記号を使うわけです。

※実際にtanのグラフをみると、90°手前で曲線がぐんぐん上へ伸びていきます。この部分が限りなく大きい数になっていく様子を表しています。

では話を戻しましょう。

$tan90°=(直線OPの傾き)=\frac{(yの増加量)}{(xの増加量)}\quad=\frac{1}{0}=\infty$

で良いでしょうか？

答えはNoです。

“傾き $\frac{4}{3}$ ”と”傾き∞ “との間で決定的に違うことがあります。

それは「値が定まっているか」という点です。

ちゃんと目盛りが打ってある数直線上において、 $\frac{4}{3}$ という数字はここ！

と指させるのに対し ∞は無理ですよね。数直線をどこまで延長してもここ！とは言えないのです。

f:id:sarugorirag:20190815104559j:plain

傾きとは直線の状態をを表現する尺度であり、それを用いて他の数値を計算したりします。そんな数値が、数直線上で指させないようなぼんやりとしたものではいけません。よって、tan90°の値は「無し」ということになるのです。

tan90°の値が決まらないということをもう少しお話ししましょう。

先ほど分母をどんどん小さくしていってtan90°としたときは分母分子共に正の数でしたから、90°より小さい角度の方から87°,88°,89°…と90°に近づけたわけですが(下図の赤文字)

f:id:sarugorirag:20190815111330j:plain

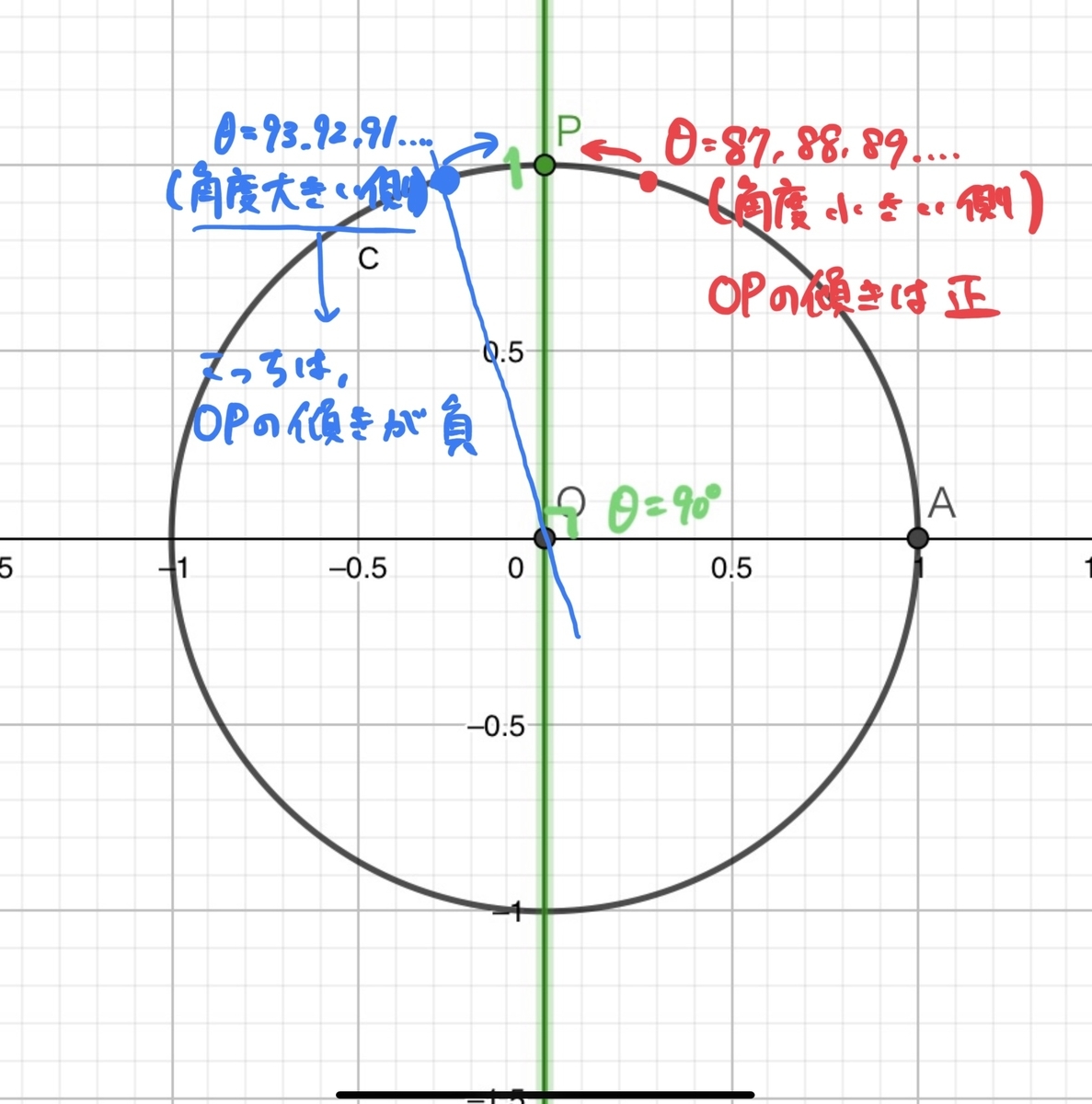
青文字のように逆サイド(90°より大きい角度のほう)から90°に近づくこともできるはずです。この場合、傾きは負の数となっていることに注意してください。するとこちら側では93°,92°,91°…と90°に近づくに連れて傾きが限りなく小さな値になっていくのがわかりますか？

式にするとこうなります。

赤: $\displaystyle \lim_{\theta\to90°-0}tan(\theta)=\infty$

(訳:θを90°より小さい側から90°に近づけると、tanθは限りなく大きい値になります)

青: $\displaystyle \lim_{\theta\to90°+0}tan(\theta)=-\infty$
(訳:θを90°より大きい側から90°に近づけると、tanθは限りなく小さい値になります)

どちらもtan90°の値を求めようとしているのに、片方は∞、もう片方は-∞と真逆の結果になっています。変ですよね。このことからも、tan90°の値は定まらないということを感じてもらえると嬉しいです。

ついつい話が難しくなってしまいましたが、要するに「tan90°はとてもややこしいので考えないようにしましょう」ということです。

結局そんだけかい！と思うかもしれませんが「なぜ考えないのか」という部分、今回の記事の内容を知っておくことに意味があるのではないかと思う医学生Gでした(^^)

2019-08-10

#13 (90°±θ)、(180°±θ)の問題を解く

〜高1

　こんにちは、医学生Gです。今回の記事はつまずく人が多いと思われる (90°±θ)、(180°±θ)みたいな角度の三角比について話をしていこうかと思います。

　この (90°±θ)、(180°±θ)、知ってる人もいるかとは思いますが、暗記しなくても導くことができるのです。実際暗記の嫌いな私も導いて考えていましたので是非参考にしてみてください。

1)〜4)の例題を通してその手順を説明していきます。

＊今回は0)〜4)まであります。図が手書きのため、読みにくかったらすみません。

0)単位円の定義の復習

f:id:sarugorirag:20190727115056p:plain

　上の図のような半径1の単位円において、点Aを座標(1,0)、点Pを単位円周上の点で、 $\angle{POA}=\theta$ として、この時の点Pの座標を(cosθ,sinθ)と定義しましたね。覚えていましたか？以下、これを使ってやりますので記憶が曖昧！って人は#11を確認してください。

1)cos(90°-θ)

f:id:sarugorirag:20190805234210p:plain

　上の図を参考にしながら6つのステップで解いていきましょう。

＊点Aの座標を（cosθ,sinθ）としておきますね。

①90°-θの点はどこか

　90°からθを引いた角度の点ですよね。単位円上の点をy軸からθだけ時計回りに動かした点、上図だと点Cのことです。

②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る

　点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形CODの2つの直角三角形ができましたね。

③合同な三角形を見つけよう

　先ほど作った直角三角形は実は合同な三角形であり△OAB≡△CODとなります。

どちらも内角が 90°,θ,(90°-θ) となっています。確認してみてください。

④求めたい数値と同じ値となる辺を探す

　今回はcos(90°-θ)の値が知りたいですので点Cのx座標の値と同じになる辺を探してくれば良いのです。(cosはx座標として定義されるんでしたよね。) そうなると辺ODの長さが点Cのx座標の値と一致しますよね。ということは、合同な三角形である△OABにおける辺ABの値とも一致します。

⑤ ④で見つけた辺の長さを求める

　辺ODの長さは辺ABの長さと一致しているというのは④でわかりました。辺ABの長さは点Aのy座標の値と一致してますので、AB=sinθ

AB=ODよりOD=sinθ と分かります。

⑥ ⑤で見つけた値と今求めようとしている値を一致させる

　今求めたいのはcos(90°-θ)の値、つまり点Cのx座標の値です。④でも書いてる通り点Cのx座標の値は辺ODの長さと一致します。つまり、⑤より cos(90°-θ)=OD=sinθ となります。

　長々と①〜⑥まで書きましたが慣れてくると10秒くらいでできますので是非参考にしてください。

2)sin(180°-θ)

f:id:sarugorirag:20190806001009p:plain

　上図を参考にして1)と同じことをしていきます。

＊点Aの座標を（cosθ,sinθ）としておきますね。

①180°-θの点はどこか

180°-θはx軸からθだけ時計回りに引いた上図の点Cのところになります。

②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る

　点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形OCDの2つの直角三角形ができましたね。

③合同な三角形を見つけよう

　今回の合同な三角形は △OABと△OCD です。

④ 今求めたい数値と同じ値となる辺を探す

　今回はsin(180°-θ)の値が知りたいですので点Cのy座標の値と同じになる辺を探してくれば良いのです。そうなると辺CDの長さが点Cのy座標の値と一致しますよね。ということは、合同な三角形である△OABにおける辺ABの値とも一致します。

⑤ ④で見つけた辺の長さを求める

　辺CDの長さは辺ABの長さと一致しているというのは④でわかりました。辺ABの長さは点Aのy座標の値と一致してますので、AB=sinθ

AB=CDよりCD=sinθとなります。

⑥ ⑤で見つけた値と今求めようとしている値を一致させる

　今求めたいのはsin(180°-θ)、つまり点Cのy座標の値です。④でも書いてる通り点Cのy座標の値は辺CDの長さと一致します。つまり、⑤よりsin(180°-θ)=CD=sinθになりますね。

3)cos(90°+θ)

f:id:sarugorirag:20190806002511p:plain

　上図を参考にしてまた同じことをいていきます。

＊点Aの座標を（cosθ,sinθ）としておきますね。

①90°+θの点はどこか

　90°+θは元の△OABの $\angle{AOB}=θ$ に90°だけ足した点です。上図の点Cがそうですね。

②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る

　点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形OCDの2つの直角三角形ができましたね。

③合同な三角形を見つけよう

　今回の合同な三角形は△OABと△COD です。

④今求めたい数値と同じ値となる辺を探す

　今回はcos(90°+θ)の値が知りたいですので点Cのx座標の絶対値と同じになる辺を探してくれば良いのです。なぜ今回は絶対値をとるかと言いますと、点Cのx座標の値は今回はマイナスであり、辺の長さにマイナスは存在しないからです。なんとなくわかってもらえればかまいません。すると辺ODの長さが点Cのx座標の絶対値と一致しますよね。ということは、合同な三角形である△OABでいう辺ABの値とも一致します。

⑤ ④で見つけた辺の長さを求める

　辺ODの長さは辺ABの長さと一致しているというのは④でわかりました。辺ABの長さは点Aのy座標の値と一致してますので、AB=sinθ、AB=ODよりOD=sinθとなります。

⑥ ⑤で見つけた値と今求めようとしている値を一致させる

　今求めたいのはcos(90°+θ)、つまり点Cのx座標の絶対値です。④でも書いてる通り点Cのx座標の値は辺ODの長さと一致します。ただし、cos(90°+θ)の座標は負の値ですのでここでマイナスをつけるのを忘れないようにしましょう。今回は、⑤よりcos(90°+θ)=-OD=-sinθになりますね。

　0°<θ<180°の範囲だったらsinの方は常に正の値ですので、何も考えずに辺の長さで求めることができますが、cosは90°<θ<180°の範囲は負の値を取りますので、もし最初に置いた点が負のところにあったら最後にマイナスを付け忘れないように注意しましょう。

4)tan(90°-θ)

f:id:sarugorirag:20190805234210p:plain

　tanはsin、cosと違って座標じゃないからできないじゃん！って思った人いますか？そんな人も心配しなくて大丈夫！ほとんど同じやり方でtanも求めることができます。

まず、tanの値は何かと言いますとtanは傾きの大きさです。上図で言いますとtanθの値はOAの傾きと一致します。今回はこれを利用していきます。やる過程はだいたい一緒ですので同じところは軽く飛ばしてもらっても大丈夫です。④からちょっと違います。

①90°-θの点はどこか

　90°からθを引いた所の点ですよね。単位円上の点をy軸からθだけ時計回りに動かした点、上図だと点Cのことです。

②点Aと先ほど置いた点Cから垂線を下ろして直角三角形を作る

　点Aと点Cから下ろした垂線の足をそれぞれ点B、点Dとすると三角形OABと三角形CODの2つの直角三角形ができましたね。

③合同な三角形を見つけよう

　先ほど作った直角三角形は実は合同な三角形であり△OAB≡△CODとなります。

④今求めたい傾きと同じ値となる辺を探す

　今回はtan(90°-θ)の値が知りたい。tan(90°-θ)は上図のOCの傾きですね。 $OCの傾き=\frac{DC}{OD}$ ですので、今回知りたい辺の長さはDCとODの長さです。△OAB≡△CODですので、DC=BO、OD=AB といえますね。

⑤ ④で見つけた辺の長さを求める

　辺DCの長さは辺BOと、辺ODの長さは辺ABの長さと一致しているというのは④でわかりました。辺BOの長さは点Aのx座標の値と、辺ABの長さは点Aのy座標の値と一致してますので、BO=cosθ、AB=sinθ、よって DC=cosθ、OD=sinθとなります。

⑥ ⑤で見つけた値と今求めようとしている値を一致させる

　今求めたいのはtan(90°-θ)の値であり、それは上図のOCの傾きのこと。

よって $OCの傾き=\frac{DC}{OD}=\frac{OB}{AB}=\frac{cosθ}{sinθ}=\frac{1}{tanθ}$ となります。

　tanもだいたい同じやり方でできましたね。

　tanはもう1つ求め方がありまして、前の記事にも書いたと思いましたが

$tanθ=\frac{sinθ}{cosθ}$

ですので、例えばtan(90°-θ)の値だったら、

$tan(90°-θ)=\frac{sin(90°-θ)}{cos(90°-θ)}=\frac{cosθ}{sinθ}=\frac{1}{tanθ}$

と求めることもできます。tanは自分の好きな方で求めると良いかと思います。

ここまでで紹介した①〜⑥の手順で例題以外のパターンにも対応できると思います。

5)加法定理

図で考えるのが苦手だよー！！勘弁してくれーって思った人もいるかと思います。そんな人は加法定理で解いてしまいましょう。実際私も加法定理でやってた時期がありました。加法定理についての詳しい説明は次の記事で説明しようと思っていますので、すみませんが今回は割愛させてもらいます。

$cos(90°-θ)=cos90°cosθ+sin90°sinθ=0\cdot{cosθ}+1\cdot{sinθ}=sinθ$

みたいな感じで解けます。

　今回は (90°±θ)、(180°±θ)の話をさせてもらいました。基本は単位円で合同な三角形を使って考えます。元の角度と値を求めたい角度2つの三角形を書いて考えていきましょう。どうしても図が苦手な人は次の記事に説明する加法定理を使っていいと思います。今回の記事を読んで (90°±θ)、(180°±θ)関連の問題を克服してくれると嬉しいです。

医学生Gの数学ノート

スキマ時間で読める数学の記事を数学塾講師経験のあるメンバーがお届けします！

#17 三角関数公式のレシピ

#16 合成公式はsinだけじゃないんです！

#15.5【2020年度大学入試予想問題】

＃15 加法定理その２　遊んで加法定理を理解しよう！

#14 加法定理登場！その１

#13.5 tanのグラフはなぜ途切れるのか

#13 (90°±θ)、(180°±θ)の問題を解く